Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T14:42:38.109Z Has data issue: false hasContentIssue false
  • English
  • Français

The distribution of k-free numbers and the derivative of the Riemann zeta-function

Published online by Cambridge University Press:  08 July 2016

XIANCHANG MENG
XIANCHANG MENG*
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1409 West Green Street, Urbana, IL 61801, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Under the Riemann Hypothesis, we connect the distribution of k-free numbers with the derivative of the Riemann zeta-function at nontrivial zeros of ζ(s). Moreover, with additional assumptions, we prove the existence of a limiting distribution of 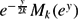$e^{-\frac{y}{2k}}M_k(e^y)$ and study the tail of the limiting distribution, where 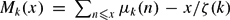$M_k(x)=\sum_{n\leq x}\mu_k(n)-{x}/{\zeta(k)}$ and μk(n) is the characteristic function of k-free numbers. Finally, we make a conjecture about the maximum order of Mk(x) by heuristic analysis on the tail of the limiting distribution.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 162 , Issue 2 , March 2017 , pp. 293 - 317
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Akbary, A., Ng, N. and Shahabi, M. Limiting distributions of the classical error terms of prime number theory. Quarterly J. Math., 65, no. 3 (2014), 743–780.Google Scholar
[2] Baker, R. C. and Pintz, J. The distribution of squarefree numbers. Acta Arith. 46 (1985), no. 1, 73–79.CrossRefGoogle Scholar
[3] Baker, R. C. and Powell, K. The distribution of k-free numbers. Acta Math. Hungar. 126 (1–2) (2010), 181–197.Google Scholar
[4] Besicovitch, A. S. On generalised almost periodic functions. Proc. London Math. Soc. (2), 25 (1926), 495–512.Google Scholar
[5] Besicovitch, A. S. Almost Periodic Functions (Cambridge University Press, 1932).Google Scholar
[6] Davenport, H. Multiplicative Number Theory. Third edition. Revised and with a preface by Hugh L. Montgomery. Graduate Texts in Mathematics, 74 (Springer-Verlag, New York, 2000).Google Scholar
[7] Evelyn, C. J. A. and Linfoot, E. H. On a problem in the additive theory of numbers IV. Ann. of Math. 32 (1931), 261–270.CrossRefGoogle Scholar
[8] Gonek, S. M. On negative moments of the Riemann zeta-function. Mathematika 36 (1989), 71–88.Google Scholar
[9] Gonek, S. M. The second moment of the reciprocal of the Riemann zeta-function and its derivative. Talk at Mathematical Sciences Research Institute, Berkeley (June 1999).Google Scholar
[10] Graham, S. W. The distribution of sqaurefree numbers. J. London Math. Soc. 28 (2) 24 (1981), no. 1, 54–64.Google Scholar
[11] Graham, S. W. and Pintz, J. The distribution of r-free numbers. Acta Math. Hungar. 53 (1989), no. 1–2, 213–236.Google Scholar
[12] Hattori, T. and Matsumoto, K. Large deviations of Montgomery type and its application to the theory of zeta-functions. Acta Arith. 71, Issue 1 (1995), 79–94.Google Scholar
[13] Hejhal, D. On the distribution of log|ζ'(1/2 + it)|. Number theory, trace formula and discrete groups (ed. Aubert, K. E., Bombieri, E. and Goldfeld, D.), (Academic Press, San Diego, 1989), 343–370.Google Scholar
[14] Hoeffding, W. Probability inequalities for sums of bounded random variables. J. Amer. Statis. Assoc., Vol. 58, No. 301 (Mar., 1963), pp. 13–30.Google Scholar
[15] Hughes, C. P., Keating, J. P. and O'Connell, N. Random matrix theory and the derivative of the Riemann zeta-function. Proc. Roy. Soc. London A 456 (2000), 2611–2627.Google Scholar
[16] Ivić, A. The Riemann Zeta-Function: theory and applications (Dover Publications, 2003).Google Scholar
[17] Jia, C. The distribution of squarefree numbers. Beijing Daxue Xuebao (1987), no. 3, 21–27.Google Scholar
[18] Jia, C. The distribution of square-free numbers. Sci. China Ser. A 36 (1993), no. 2, 154–169.Google Scholar
[19] Montgomery, H. L. The zeta function and prime numbers. Proceedings of the Queen's Number Theory Conference 1979 (ed. Ribenboim, P., Queen's University, Kingston, ON, 1980), 1–31.Google Scholar
[20] Montgomery, H. L. and Vaughan, R. C. Hilbert's inequality. J. London Math. Soc. (2) 8 (1974), 73–82.Google Scholar
[21] Montgomery, H. L. and Vaughan, R. C. The distribution of squarefree numbers. Recent Progress in Analytic Number Theory, Vol 1 (Durham, 1979), (Academic press, London-New York, 1981), pp. 247–256.Google Scholar
[22] Ng, N. The distribution of the summatory function of the Möbius function. Proc. London Math. Soc. (3) 89 (2004), 361–389.Google Scholar
[23] Pappalardi, F. A survey on k-freeness, Number Theory, Ramanujan Math. Sec. Lecture. Notes Ser., vol 1 (Ramanujan Math. Soc., Mysor 2005), pp. 71–88.Google Scholar
[24] Sándor, J., Mitrinović, D. S. and Crstici, B. Handbook of Number Theory I, 2nd printing (Springer 2006).Google Scholar
[25] Titchmarsh, E. C. The Theory of the Riemann Zeta-function, second edition, revised by Heath–Brown, D. R. (Clarendon Press Oxford, 1986).Google Scholar
[26] Tsang, K. M. Some Ω-theorems for the Riemann zeta-function. Acta Arith. 46 (1986), no. 4, 369–395.Google Scholar
[27] Walfisz, A. Weylsche Exponentialsummen in der neueren Zahlentheorie. Mathematische Forschungsberichte, XV (VEB Deutscher Verlag der Wissenschaften, Berlin 1963).Google Scholar