Published online by Cambridge University Press: 24 October 2008
Let Mm be a closed connected smooth manifold of dimension m, and set Pm = Mm – int Dm where Dm is a disc in M. In (4), Wall has the following exact sequence
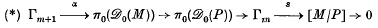
where 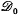 (M), (resp.
(M), (resp. 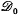 (P)) is the Δ-set of diffeomorphisms of M (resp. P) as in(l), and [M/P] is the set of diffeomorphism classes of smooth manifolds obtained by glueing a disc to the boundary of P. In this paper we obtain some results on π0(
(P)) is the Δ-set of diffeomorphisms of M (resp. P) as in(l), and [M/P] is the set of diffeomorphism classes of smooth manifolds obtained by glueing a disc to the boundary of P. In this paper we obtain some results on π0(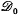 (M)) for particular M, and in the following sense: Using the techniques of (2), we can determine π0(
(M)) for particular M, and in the following sense: Using the techniques of (2), we can determine π0(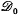 (P)), so the main portion of the paper is concerned with a discussion of the kernel of α. There is a map ω: π1(
(P)), so the main portion of the paper is concerned with a discussion of the kernel of α. There is a map ω: π1(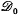 (P)) → Γm+1, given by the obstruction to extending h∈π1(
(P)) → Γm+1, given by the obstruction to extending h∈π1(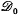 (P)) to a concordance of the identity of M to itself, and it is clear that if this map is attached at the beginning of the sequence (*) we get exactness. We will obtain (for certain M) an alternative description of the image of α in terms of those homotopy spheres which can appear as the boundaries of thickenings.
(P)) to a concordance of the identity of M to itself, and it is clear that if this map is attached at the beginning of the sequence (*) we get exactness. We will obtain (for certain M) an alternative description of the image of α in terms of those homotopy spheres which can appear as the boundaries of thickenings.