Curves of Small Genus on Certain K3 Surfaces
Published online by Cambridge University Press: 11 March 2016
Extract
Recent workers [1, 3] have proved density theorems about the rational points on K3 surfaces of the form
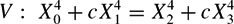 $$
V:\;X_0^4+cX_1^4=X_2^4+cX_3^4
$$
$$
V:\;X_0^4+cX_1^4=X_2^4+cX_3^4
$$
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 1 , July 2016 , pp. 103 - 106
- Copyright
- Copyright © Cambridge Philosophical Society 2016
References
REFERENCES
- 1
- Cited by


