A lattice-ordered group is a group and a lattice such that the group operation distributes through the lattice operations (i.e. f(g ∨ h)k = fgk ∨ fhk and dually). Lattice-ordered groups are torsion-free groups and distributive lattices. They further satisfy f ∧ g = (f−1 ∨ g−1)−1 and f ∨ g = (f−1 ∧ g−1)−1. Since the lattice is distributive, each lattice-ordered group word can be written in the form ∨A ∧B ωαβ where A and B are finite and each ωαβ is a group word in {xi: i ∈ I}. Unfortunately, even for free lattice-ordered groups, this form is not unique. We will use the prefix l- for maps between lattice-ordered groups that preserve both the group and lattice operations, and e for the identity element. A presentation (xi;rj(x) = e)i∈I, j∈J is the quotient of the free lattice-ordered group F on {xi: i∈I} by the l-ideal (convex normal sublattice subgroup) generated by its subset {rj(x): j ∈ J}. {xi: i ∈ I} is called a generating set and {ri(x):j∈J} a defining set of relations. If I and J are finite we have a finitely presented lattice-ordered group. If 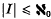we can effectively enumerate all lattice-ordered group words r1(x), r2(x),… in xi; i∈I}. If I is finite and J (for this enumeration) is a recursively enumerable set, we say that we have a recursively presented lattice-ordered group. Throughout Z denotes the group of integers and ℝ the real line.

Our purpose in this paper is to prove the natural analogues of three theorems from combinatorial group theory (5), chapter IV, theorems 4·9, 3·1 and 3·5-in particular, theorem C is a natural analogue of an unpublished theorem of Philip Hall (4).