Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T13:22:25.967Z Has data issue: false hasContentIssue false
  • English
  • Français

A correction to a paper on the dimension of Cartesian product sets

Published online by Cambridge University Press:  24 October 2008

H. G. Eggleston
H. G. Eggleston
Affiliation:
University College, Swansea
Get access Rights & Permissions [Opens in a new window]

Extract

Let Em and En be orthogonal Euclidean spaces of dimensions m and n respectively and with the origin of each as their only common point. In a previous paper (3) I gave what was intended to be a proof of the relation

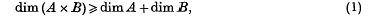
where the dimension of A, dim A, is the Besicovitch dimension, i.e. the number s such that the Hausdorff measure in any dimension greater than s is zero whilst that in any dimension less than s is infinite, where A and B are subsets of En and Em respectively and where A × B is the Cartesian product of A with B.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 49 , Issue 3 , July 1953 , pp. 437 - 440
Copyright
Copyright © Cambridge Philosophical Society 1953

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Besicovitch, A. S.Concentrated and rarefied sets of points. Acta math., Stockh., 62 (1933), 289–300.CrossRefGoogle Scholar
(2)Besicovitch, A. S. and Moran, P. A. P.The measure of product and cylinder sets. J. Lond. math. Soc. 20 (1937), 18–25.CrossRefGoogle Scholar
(3)Eggleston, H. G.The Besicovitch dimension of Cartesian product sets. Proc. Camb. phil. Soc. 46 (1950), 383–6.CrossRefGoogle Scholar
(4)Hewitt, E. and Kôsaku, Yosida.Finitely additive measures. Trans. Amer. math. Soc. 72 (1952), 46–66.Google Scholar
(5)Horn, A. and Hodges, J. L.On Maharam's conditions for measures. Trans. Amer. math. Soc. 64 (1948), 594–5.Google Scholar
(6)Horn, A. and Tarski, A.Measures in Boolean algebras. Trans. Amer. math. Soc. 64 (1948), 467–97.CrossRefGoogle Scholar
(7)Maharam, Dorothy.An algebraic characterization of measure algebras. Ann. Math., Princeton, 48 (1947), 154–68.CrossRefGoogle Scholar