Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T14:06:38.294Z Has data issue: false hasContentIssue false
  • English
  • Français

A convolution-integral representation for a class of linear operators

Published online by Cambridge University Press:  24 October 2008

K. Rowlands
K. Rowlands
Affiliation:
Department of Pure Mathematics, University College of Wales, Aberystwyth
Get access Rights & Permissions [Opens in a new window]

Extract

Let 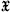be the complex vector space consisting of all complex-valued functions of a non-negative real variable t. For each positive number u, the shift operator Iu is the mapping of 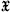into itself defined by the formula

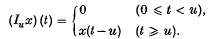
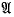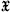A linear operator T which maps a subspace of into itself is said to be a V-operator (13) if:

(a) for each x in 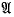, the complex-conjugate function x* is in ;

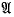(b) both 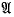and 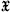\ 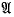are invariant under the shift operators;

(c) every shift operator commutes with T.

(Property (a) ensures that every function x in 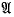can be uniquely expressed as x1 + ix2, where x1 and x2 are real functions in .)

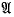Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 71 , Issue 1 , January 1972 , pp. 51 - 60
Copyright
Copyright © Cambridge Philosophical Society 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Banach, S.Théorie des opérations linéaires (Warsaw, 1932).Google Scholar
(2)Bertz, E.Operatorenrechnung auf funkionalanalytischer Grundlage. Math. Z. 88 (1965), 1–39.CrossRefGoogle Scholar
(3)Boehme, T. K.Continuity and perfect operators. J. London Math. Soc. 39 (1964), 355–358.CrossRefGoogle Scholar
(4)Edwards, R. E.Representation theorems for certain functional operators. Pacific J. Math. 7 (1957), 1333–1339.CrossRefGoogle Scholar
(5)Hewitt, E. and Stromberg, K.Real and abstract analysis (Springer-Verlag, 1965).Google Scholar
(6)Horváth, J.Topological vector spaces and distributions (Vol. 1). (Addison-Wesley, 1966).Google Scholar
(7)Johnson, B. E.An introduction to the theory of centralizers. Proc. London Math. Soc. (3), 14(1964), 299–320.CrossRefGoogle Scholar
(8)Johnson, B. E.Centralizers on certain topological algebras. J. London Math. Soc. 39 (1964), 603–614.CrossRefGoogle Scholar
(9)Rowlands, K.Some new characterizations of perfect operators. J. London Math. Soc. 44 (1969), 531–541.CrossRefGoogle Scholar
(10)Schwartz, L.Théorie des distributions (Tome 1). Actualités Scientifiques et Industrielles 1245 (Hermann, Paris, 1957).Google Scholar
(11)Weston, J. D.Characterizations of Laplace transforms and perfect operators. Arch. Rational Mech. Anal. 3 (1959), 348–354.CrossRefGoogle Scholar
(12)Weston, J. D.Positive perfect operators. Proc. London Math. Soc. (3), 10 (1960), 545–565.CrossRefGoogle Scholar
(13)Weston, J. D.On the representation of operators by convolution integrals. Pacific J. Math 10 (1960), 1453–1468.CrossRefGoogle Scholar
(14)Zaanen, A. C.Integration (Revised Edition) (North Holland Publishing Co., 1967).Google Scholar