Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T13:42:29.309Z Has data issue: false hasContentIssue false
  • English
  • Français

A conjecture of Fejes Tóth on saturated systems of circles

Published online by Cambridge University Press:  24 October 2008

Vishwa Chander Dumir  and
Dharam Singh Khassa
Vishwa Chander Dumir
Affiliation:
Department of Mathematics, Punjab University, Chandigarh 14, India
Dharam Singh Khassa
Affiliation:
Department of Mathematics, Punjab University, Chandigarh 14, India
Get access Rights & Permissions [Opens in a new window]

Extract

A family ℳ of closed circular discs in the plane is called a saturated family or a saturated system of circles if (i) the infimum r of the radii of the discs in ℳ is positive and (ii) every closed disc of radius r in the plane intersects at least one disc in ℳ. For a saturated family ℳ, we denote by S the point-set union of the interiors of the members of ℳ and by S(l) the part of S inside the circular disc of radius l centred at the origin. We define the lower density ρℳ of the saturated family ℳ as

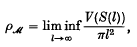
where V(S(l)) denotes the Lebesgue measure of the set S(l).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 3 , November 1973 , pp. 453 - 460
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bambah, R. P., Rogers, C. A. and Zassenhaus, H.On coverings with convex domains. Acta Arith. 9 (1964), 191–207.CrossRefGoogle Scholar
(2)Bambah, R. P. and Woods, A. C.On minimal density of the plane coverings by circles. Acta Math. Acad. Sci. Hungar. 19, 3–4 (1968), 337–343.CrossRefGoogle Scholar
(3)Bambah, R. P. and Woods, A. C.The covering constant for a cylinder. Monatsh. Math. 72 (1968), 107–117.CrossRefGoogle Scholar
(4)Coxeter, H. S. M., Few, L. and Rogers, C. A.Covering space with equal spheres. Mathematika 6 (1959), 147–157.CrossRefGoogle Scholar
(5)Eggleston, H. G.A minimal density plane covering problem. Mathematika 12 (1965), 226–234.CrossRefGoogle Scholar
(6)Fejes, TóTh, L. Packings and coverings in the plane. Proc. Coll. Convexity, Copenhagen, 1965 (1967), 78–87.Google Scholar