Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shparlinski, Igor E.
and
Yau, Kam-hung
2016.
Bounds of double multiplicative character sums and gaps between residues of exponential functions.
Journal of Number Theory,
Vol. 167,
Issue. ,
p.
304.
Felix, Adam Tyler
and
Kurlberg, Pär
2017.
On the fixed points of the map x↦x modulo a prime, II.
Finite Fields and Their Applications,
Vol. 48,
Issue. ,
p.
141.
Shteinikov, Yurii N.
2017.
On the product sets of rational numbers.
Proceedings of the Steklov Institute of Mathematics,
Vol. 296,
Issue. 1,
p.
243.
Garaev, M. Z.
2018.
On Distribution of Elements of Subgroups in Arithmetic Progressions Modulo a Prime.
Proceedings of the Steklov Institute of Mathematics,
Vol. 303,
Issue. 1,
p.
50.
Shkredov, Ilya D.
and
Shparlinski, Igor E.
2018.
Double Character Sums with Intervals and Arbitrary Sets.
Proceedings of the Steklov Institute of Mathematics,
Vol. 303,
Issue. 1,
p.
239.
Shteinikov, Yurii N.
2018.
On the Size of the Quotient of Two Subsets of Positive Integers.
Proceedings of the Steklov Institute of Mathematics,
Vol. 303,
Issue. 1,
p.
259.
Garaev, M.Z.
2019.
Double exponential sums and congruences with intervals and exponential functions modulo a prime.
Journal of Number Theory,
Vol. 199,
Issue. ,
p.
377.
Friedrichsen, Matthew
and
Holden, Joshua
2019.
Statistics for fixed points of the self-power map.
Involve, a Journal of Mathematics,
Vol. 12,
Issue. 1,
p.
63.
Macourt, Simon
Petridis, Giorgis
Shkredov, Ilya D.
and
Shparlinski, Igor E.
2020.
Bounds of Trilinear and Trinomial Exponential Sums.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 4,
p.
2124.
Holden, Joshua
Richardson, Pamela A.
and
Robinson, Margaret M.
2020.
Counting Fixed Points and Rooted Closed Walks of the Singular Map $$x \mapsto {x^{{x^n}}}$$ Modulo Powers of a Prime.
p-Adic Numbers, Ultrametric Analysis and Applications,
Vol. 12,
Issue. 1,
p.
12.
Di Benedetto, Daniel
Garaev, Moubariz Z.
Garcia, Victor C.
Gonzalez-Sanchez, Diego
Shparlinski, Igor E.
and
Trujillo, Carlos A.
2020.
New estimates for exponential sums over multiplicative subgroups and intervals in prime fields.
Journal of Number Theory,
Vol. 215,
Issue. ,
p.
261.
Chen, Bo
2022.
Explicit upper bound on the least primitive root modulo p2.
International Journal of Number Theory,
Vol. 18,
Issue. 02,
p.
389.
Shparlinski, Igor E.
2023.
Fixed points of the subset sum pseudorandom number generators.
Designs, Codes and Cryptography,
Vol. 91,
Issue. 7,
p.
2473.
Garaev, Moubariz Z.
and
Shparlinski, Igor E.
2024.
On some congruences and exponential sums.
Finite Fields and Their Applications,
Vol. 98,
Issue. ,
p.
102451.
Garaev, Moubariz Z.
Rudnick, Zeev
and
Shparlinski, Igor E.
2024.
On a family of sparse exponential sums.
Mathematische Nachrichten,
Vol. 297,
Issue. 11,
p.
4214.
Wang, Jiankang
and
Xu, Zhefeng
2024.
Double and triple character sums and gaps between the elements of subgroups of finite fields.
International Journal of Number Theory,
Vol. 20,
Issue. 07,
p.
1725.
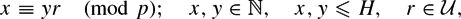 $$\begin{equation}
x\equiv y r\pmod p;\quad x,y\in \mathbb{N},\quad x,y\le H,\quad r\in \mathcal{U},
\end{equation}$$
$$\begin{equation}
x\equiv y r\pmod p;\quad x,y\in \mathbb{N},\quad x,y\le H,\quad r\in \mathcal{U},
\end{equation}$$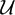 ${\mathcal U}$|, where
${\mathcal U}$|, where 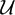 ${\mathcal U}$ is a subset of the field of residue classes modulo p having small multiplicative doubling. We then use these estimates to show that the number of solutions of the congruence
${\mathcal U}$ is a subset of the field of residue classes modulo p having small multiplicative doubling. We then use these estimates to show that the number of solutions of the congruence
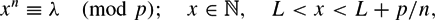 $$\begin{equation}
x^n\equiv \lambda\pmod p; \quad x\in \mathbb{N}, \quad L<x<L+p/n,
\end{equation}$$
$$\begin{equation}
x^n\equiv \lambda\pmod p; \quad x\in \mathbb{N}, \quad L<x<L+p/n,
\end{equation}$$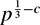 $p^{\frac{1}{3}-c}$ uniformly over positive integers n, λ and L, for some absolute constant c > 0. This implies, in particular, that if f(x) ∈
$p^{\frac{1}{3}-c}$ uniformly over positive integers n, λ and L, for some absolute constant c > 0. This implies, in particular, that if f(x) ∈ 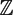 $\mathbb{Z}$[x] is a fixed polynomial without multiple roots in
$\mathbb{Z}$[x] is a fixed polynomial without multiple roots in 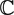 $\mathbb{C}$, then the congruence xf(x) ≡ 1 (mod p), x ∈
$\mathbb{C}$, then the congruence xf(x) ≡ 1 (mod p), x ∈ 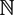 $\mathbb{N}$, x ⩽ p, has at most
$\mathbb{N}$, x ⩽ p, has at most 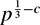 $p^{\frac{1}{3}-c}$ solutions as p → ∞, improving some recent results of Kurlberg, Luca and Shparlinski and of Balog, Broughan and Shparlinski. We use our results to show that almost all the residue classes modulo p can be represented in the form xgy (mod p) with positive integers x < p5/8+ϵ and y < p3/8. Here g denotes a primitive root modulo p. We also prove that almost all the residue classes modulo p can be represented in the form xyzgt (mod p) with positive integers x, y, z, t < p1/4+ϵ.
$p^{\frac{1}{3}-c}$ solutions as p → ∞, improving some recent results of Kurlberg, Luca and Shparlinski and of Balog, Broughan and Shparlinski. We use our results to show that almost all the residue classes modulo p can be represented in the form xgy (mod p) with positive integers x < p5/8+ϵ and y < p3/8. Here g denotes a primitive root modulo p. We also prove that almost all the residue classes modulo p can be represented in the form xyzgt (mod p) with positive integers x, y, z, t < p1/4+ϵ.