Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T12:20:12.994Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence properties of the partition function and associated functions

Published online by Cambridge University Press:  24 October 2008

J. M. Rushforth
J. M. Rushforth
Affiliation:
The UniversityBirmingham
Get access Rights & Permissions [Opens in a new window]

Extract

The subject of this paper is the study of an unpublished manuscript by the late Srinivasa Ramanujan, the Indian mathematician. The manuscript covers forty-three pages of foolscap, and it is now in the possession of Prof. G. N. Watson. It is entitled

‘Properties of p(n) and τ(n) defined by the relations

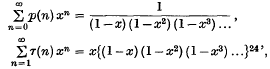
and was sent to the late Prof. G. H. Hardy by Ramanujan a few months before the latter's death in 1920. The work in the manuscript is concerned with the congruence properties of p(n) and τ(n), and Hardy extracted from it (Ramanujan (16)) proofs of the theorems

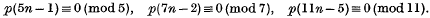
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 3 , July 1952 , pp. 402 - 413
Copyright
Copyright © Cambridge Philosophical Society 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bambah, R. P.Two congruence properties of Ramanujan's function τ(n). J. Lond. math. Soc. 21 (1946), 91–3.CrossRefGoogle Scholar
(2)Bambah, R. P.Ramanujan's function τ(n)—a congruence property. Bull. Amer. math. Soc. 53 (1947), 764–5.CrossRefGoogle Scholar
(3)Bambah, R. P. and Chowla, S.A congruence property of Ramanujan's function τ(n). Proc. nat. Inst. Sci. India, 12 (1946), 431–2.Google Scholar
(4)Bambah, R. P. and Chowla, S.A new congruence property of Ramanujan's function τ(n). Bull. Amer. math. Soc. 53 (1947), 768–9.CrossRefGoogle Scholar
(5)Bambah, R. P. and Chowla, S.Congruence properties of Ramanujan's function τ(n). Bull. Amer. math. Soc. 53 (1947), 950–5.CrossRefGoogle Scholar
(6)Bambah, R. P. and Chowla, S.The residue of Ramanujan's function τ(n) to the modulus 28. J. Lond. math. Soc. 22 (1947), 140–7.CrossRefGoogle Scholar
(7)Bambah, R. P., Chowla, S., Gupta, H. and Lahiri, D. B.Congruence properties of Ramanujan's function τ(n). Quart. J. Math. 18 (1947), 143–6.CrossRefGoogle Scholar
(8)Gupta, H.A congruence property of τ(n). Proc. Indian Acad. Sci. A, 24 (1946), 441–2.CrossRefGoogle Scholar
(9)Hardy, G. H.Ramanujan (Cambridge, 1940), p. 166.Google Scholar
(10)Hardy, G. H. and Wright, E. M.The theory of numbers (Oxford, 1938), p. 282.Google Scholar
(11)Hecke, E.Über Modulfunktionen und die Dirichletschen Reihen mit Eulerscher Produktentwicklung, I. Math. Ann. 114 (1937), 1–28.CrossRefGoogle Scholar
(12)Jacobi, C. G. J.Ges. Werke, vol. 1 (Berlin, 1881), §36, equation (12), p. 146, and §41, equation (3), p. 167.Google Scholar
(13)Ramanathan, K. G.Congruence properties of Ramanujan's function τ(n), II. J. Indian math. Soc. (N.S.), 9 (1945), 55–9.Google Scholar
(14)Ramanathan, K. G.Congruence properties of Ramanujan's function τ(n). Proc. Indian Acad. Sci. A, 19 (1944), 146–8.CrossRefGoogle Scholar
(15)Ramanujan, S.On certain arithmetical functions. Trans. Camb. phil. Soc. 22 (1916), 159–84. Reprinted in The collected papers of S. Ramanujan (Cambridge, 1927), pp. 136–62.Google Scholar
(16)Ramanujan, S.Congruence properties of partitions. Math. Z. 9 (1921), 147–53. Reprinted in The collected papers of S. Ramanujan (Cambridge, 1927), pp. 232–8.CrossRefGoogle Scholar
(17)Rushforth, J. M. Congruence properties of the partition function and associated functions. Ph.D. thesis, University of Birmingham, 1950.Google Scholar
(18)Simons, W. H.Congruences involving the partition function p(n). Bull. Amer. math. Soc. 50 (1944), 883–92.CrossRefGoogle Scholar
(19)Watson, G. N.Über Ramanujansche Kongruenzeigenschaften der Zerfällungsanzahlen, I. Math. Z. 39 (1935), 712–31.CrossRefGoogle Scholar
(20)Watson, G. N.Ramanujans Vermutung über Zerfällungsanzahlen. J. reine angew. Math. 179 (1938), 97–128.CrossRefGoogle Scholar
(21)Watson, G.N.A table of Ramanujan's function τ(n). Proc. Lond. math. Soc. (2), 51 (1948), 1–13.Google Scholar
(22)Wilton, J. R.Congruence properties of Ramanujan's function τ(n). Proc. Lond. math. Soc. (2), 31 (1930), 1–10.CrossRefGoogle Scholar
(23)Zuckerman, H. S.Identities analogous to Ramanujan's identities involving the partition function. Duke math. J. 5 (1939), 88–110.CrossRefGoogle Scholar