Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T08:27:00.975Z Has data issue: false hasContentIssue false
  • English
  • Français

A congruence between link polynomials

Published online by Cambridge University Press:  24 October 2008

Lee Rudolph
Lee Rudolph
Affiliation:
Department of Mathematics and Computer Science, Clark University, Worcester, Massachusetts 01610, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

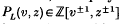Throughout, ‘link’ means ‘oriented link in S3’, and ‘polynomial’ means ‘Laurent polynomial’. Let L be a link; then denotes the oriented polynomial of L (see [2, 8]), written in Morton's variables (see [5]), and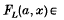 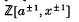denotes the semi-oriented polynomial of L (see [3]). Let L have components K1, …, Kn. The total linking of L, denoted t(L), is the sum of the linking numbers lk (Ki, Kj) with 1 ≤ i < j ≤ n. Let f be a framing of L (that is, f assigns an integer to each Ki); then f(L) denotes the total framing of L (that is, the sum of these integers), and A(L, f) denotes the naturally associated union of annuli embedded in S3 Define the framed polynomial {L, f} (v, z) to be (–1)n plus (v−1–v)z−1 times the sum, over all non-empty sublinks K of L, of 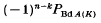(where K has k components with 1 ≤ k ≤ n).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 107 , Issue 2 , March 1990 , pp. 319 - 327
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Franks, J. and Williams, R. F.. Braids and the Jones–Conway polynomial. Trans. Amer. Math. Soc. 303 (1987), 97–108.CrossRefGoogle Scholar
[2]Freyd, P., Yetter, D., Hoste, J., Lickorish, W. B. R., Millett, K. and Ocneanu, A.. A new polynomial invariant of knots and links. Bull. Amer. Math. Soc. 12 (1985), 239–246.CrossRefGoogle Scholar
[3]Kauffman, L. H.. Formal Knot Theory. Princeton Lecture Notes no. 30 (Princeton University Press, 1987).Google Scholar
[4]Lickorish, W. B. R.. A relationship between link polynomials. Math. Proc. Cambridge Philos. Soc. 100 (1986), 109–112.CrossRefGoogle Scholar
[5]Morton, H.. Seifert circles and knot polynomials. Math. Proc. Cambridge Philos. Soc. 99 (1986), 107–110.CrossRefGoogle Scholar
[6]Neumann, Walter D. and Rudolph, Lee. Unfoldings in knot theory. Math. Ann. 278 (1987). 409–439.CrossRefGoogle Scholar
corrigendum, Math. Ann. (to appear).Google Scholar
[7]Neumann, Walter D. and Rudolph, Lee. Difference index of vector-fields and the enhanced Milnor number. Topology (to appear).Google Scholar
[8]Przytycki, J. H. and Traczyk, P.. Invariants of links of Conway type. Kobe J. Math. 4 (1987), 115–139.Google Scholar
[9]Rudolph, Lee. Algebraic functions and closed braids. Topology 22 (1983), 191–202.CrossRefGoogle Scholar
[10]Rudolph, Lee. Braided surfaces and Seifert ribbons for closed braids. Comment. Math. Helv. 58 (1983), 1–37.CrossRefGoogle Scholar
[11]Rudolph, Lee. Constructions of quasipositive knots and links, I. In Nœuds, Tresses, et Singularités, ed. Weber, C. (Kundig, 1983), pp. 233–245.Google Scholar
[12]Rudolph, Lee. Some knot theory of complex plane curves. In Nœuds. Tresses, et Singularités. ed. Weber, C. (Kundig, 1983), pp. 99–122.Google Scholar
[13]Rudolph, Lee. Constructions of quasipositive knots and links, II. Contemp. Math. 35 (1984), 485–491.CrossRefGoogle Scholar
[14]Rudolph, Lee. Isolated critical points of maps from ℝ4 to ℝ2 and a natural splitting of the Milnor number of a classical fibered link. Part I: Basic theory; examples. Comment. Math. Helv. 62 (1987), 630–645.CrossRefGoogle Scholar
[15]Rudolph, Lee. Quasipositivity and new knot invariants. Rev. Mat. Univ. Complutense Madrid (to appear).Google Scholar
[16]Rudolph, Lee. A characterization of quasipositive Seifert surfaces (Constructions of quasipositive knots and links, III). (Preprint, 1988.)Google Scholar
[17]Rudolph, Lee. Quasipositive plumbing (Constructions of quasipositive knots and links, V). (Preprint, 1988.)Google Scholar
[18]Yamada, S.. An operator on regular isotopy invariants of link diagrams. (Preprint, 1987.)Google Scholar