Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T13:54:26.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Conformal geodesics on gravitational instantons

Published online by Cambridge University Press:  09 July 2021

MACIEJ DUNAJSKI  and
PAUL TOD
MACIEJ DUNAJSKI
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA. e-mail: [email protected]
PAUL TOD
Affiliation:
The Mathematical Institute, Oxford University, Woodstock Road, Oxford OX2 6GG. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the integrability of the conformal geodesic flow (also known as the conformal circle flow) on the SO(3)–invariant gravitational instantons. On a hyper–Kähler four–manifold the conformal geodesic equations reduce to geodesic equations of a charged particle moving in a constant self–dual magnetic field. In the case of the anti–self–dual Taub NUT instanton we integrate these equations completely by separating the Hamilton–Jacobi equations, and finding a commuting set of first integrals. This gives the first example of an integrable conformal geodesic flow on a four–manifold which is not a symmetric space. In the case of the Eguchi–Hanson we find all conformal geodesics which lie on the three–dimensional orbits of the isometry group. In the non–hyper–Kähler case of the Fubini–Study metric on 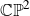$\mathbb{CP}^2$ we use the first integrals arising from the conformal Killing–Yano tensors to recover the known complete integrability of conformal geodesics.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 1 , July 2022 , pp. 123 - 154
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

References

Adachi, T.. (1995) Kähler magnetic flows for a manifold of constant holomorphic sectional curvature. Tokyo J. Math. 18, 473–483.10.3836/tjm/1270043477CrossRefGoogle Scholar
Adachi, T., Maeda, S. and Udagawa, S.. Circles in a complex projective space. Osaka J. Math. 32 (1995), 709–719.Google Scholar
Bailey, T. N. and Eastwood, M. G.. Conformal circles and parametrizations of curves in conformal manifolds. Proc. Amer. Math. Soc. 108 (1990), 215–221.Google Scholar
Bailey, T. N., Eastwood, M. G. and Gover, A. R.. Thomas’s structure bundle for conformal, projective and related structures. Rocky Mountain J. Math. 24 (1994), 1191–1217.10.1216/rmjm/1181072333CrossRefGoogle Scholar
Casey, S., Dunajski, M. and Tod, K. P.. Twistor geometry of a pair of second order ODEs Comm. Math. Phys. 321 (2013), 681–701.10.1007/s00220-013-1729-7CrossRefGoogle Scholar
Comtet, A.. On the Landau levels on the hyperbolic plane. Ann. of Phys. 173 (1987), 185–209.10.1016/0003-4916(87)90098-4CrossRefGoogle Scholar
Dunajski, M.. Solitons Instantons and Twistors. Oxford Graduate Texts in Math. (Oxford University Press, 2009).Google Scholar
Dunajski, M. and KryŃski, W.. Variational principles for conformal geodesics. (2021) arXiv: arXiv:2104.13105.Google Scholar
Dunajski, M. and Tod, K. P.. Four dimensional metrics conformal to Kahler. Math. Proc. Camb. Phil. Soc. 148 (2010), 485.10.1017/S030500410999048XCrossRefGoogle Scholar
Dunajski, M. and Tod, P.. Self-dual conformal gravity. Comm. Math. Phys. 331 (2014), 351–373.10.1007/s00220-014-2046-5CrossRefGoogle Scholar
Eguchi, T. and Hanson, A.. Selfdual solutions to Euclidean gravity. Annals of Phys 120 (1979), 82–105.10.1016/0003-4916(79)90282-3CrossRefGoogle Scholar
Frolov, V. P., Krtous, P., and Kubiznak, D.. Black holes, hidden symmetries and complete integrability. Living Revievs in Relativity (2017).10.1007/s41114-017-0009-9CrossRefGoogle Scholar
Gibbons, G. W. and Hawking, S. W.. Gravitational multi - instantons. Phys. Lett. B78 (1978), 430.10.1016/0370-2693(78)90478-1CrossRefGoogle Scholar
Gibbons, G. W. and Pope, C.. $\mathbb{CP}^2$ As a gravitational instanton. Commun. Math. Phys. 61 (1978), 239.10.1007/BF01940766CrossRefGoogle Scholar
Gibbons, G. W. and Ruback, P. J.. The hidden symmetries of multicentre metrics. Comm. Math. Phys. 115 (1988), 267–300.10.1007/BF01466773CrossRefGoogle Scholar
Gover, A. R., Snell, D. and Taghavi-Chabert, A.. Distinguished curves and integrability in Riemannian, conformal and projective geometry (2018) arXiv:1806.09830.Google Scholar
Houri, T., Takeshi, O. and Yukinori, Y.. Closed conformal Killing–Yano tensor and geodesic integrability. J. Phys. A41. (2007), 025204.10.1088/1751-8113/41/2/025204CrossRefGoogle Scholar
Joachimsthal, F.. Observationes de lineis brevissimis et curvis curvaturae in superficiebus secundi gradus JRAM 26 (1843), 155–171.Google Scholar
Landau, L. D. and Lifshitz, E.. The Classical Theory of Fields (Pergamon Press, 1962).Google Scholar
Maeda, S. and Adachi, T.. Integral curves of Killing vector fields in a complex projective space. Mem. Fac. Sci. Eng. Shimane Univ. B34 (2001), 61–85.Google Scholar
Maeda, S. and Ohnita, Y.. Helical geodesic immersion into complex space forms. Geom. Dedicata 30 (1989), 93–114.10.1007/BF02424315CrossRefGoogle Scholar
Nomizu, K. and Yano, K.. On circles and spheres in Riemannian geometry. Math. Ann. 210 (1974), 163–170.10.1007/BF01360038CrossRefGoogle Scholar
Penrose, R. and Rindler, W.. Spinors and Space-time. Two-Spinor Calculus and Relativistic Fields. Cambridge Monogr. Math. Phys. (Cambridge University Press, Cambridge, 1987, 1988).Google Scholar
Sihlan, J. and Zadnik, V. Conformal theory of curves with tractors. (2018), arXiv:1805.00422.Google Scholar
Tod, K. P.. Some examples of the behaviour of conformal geodesics. J. Geom. Phys. 62 (2012), 1778–1792.10.1016/j.geomphys.2012.03.010CrossRefGoogle Scholar
Valent, G.. Integrability Versus Separability for the Multi-Centre Metrics. Comm. Math. Phys. 244 (2004), 571–594.10.1007/s00220-003-1002-6CrossRefGoogle Scholar