No CrossRef data available.
Concerning automorphisms in finitely generated Abelian groups
Published online by Cambridge University Press: 24 October 2008
Extract
Of particular importance in the structure theory of finitely generated groups are those groups G having the property ℳd that for any two sets of generators g1, …, gd; h1, …, hd of G there is an automorphism θ of G such that 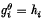 (i = 1, …, d). Gaschütz(1) proved that all groups G having† ℳd also possess a further manifestation of symmetry, the property
(i = 1, …, d). Gaschütz(1) proved that all groups G having† ℳd also possess a further manifestation of symmetry, the property  that if M and N are finite normal subgroups of G, any isomorphism between G/M and G/N can be induced by an automorphism of G. The case in which G is a finite p-group had previously been considered by Taunt (6) and Liebeck(2), who proved that for such groups the above property on the quotient groups of G is equivalent to ℳd.
that if M and N are finite normal subgroups of G, any isomorphism between G/M and G/N can be induced by an automorphism of G. The case in which G is a finite p-group had previously been considered by Taunt (6) and Liebeck(2), who proved that for such groups the above property on the quotient groups of G is equivalent to ℳd.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 1 , January 1963 , pp. 25 - 31
- Copyright
- Copyright © Cambridge Philosophical Society 1963


