Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T01:57:07.149Z Has data issue: false hasContentIssue false
  • English
  • Français

A computation of the Littlewood exponent of stochastic processes

Published online by Cambridge University Press:  24 October 2008

Ron C. Blei  and
J.-P. Kahane
Ron C. Blei
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Connecticut 06268, USA.
J.-P. Kahane
Affiliation:
Mathématique, Bát 425, Université de Paris– Sud, 91405 Orsay, France.
Get access Rights & Permissions [Opens in a new window]

Extract

A stochastic process X = {X(t): t ∈ [0, 1]} on a probability space (Ω, 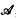, ℙ) is said to have finite expectation if the function defined on the measureable rectangles in Ω × [0, 1] by

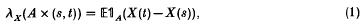
for A ∈ 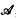and (s, t) ⊂ [0, 1] gives rise to a complex measure in each of its two coordinates (see [1], definition 1·1). Equivalently, X has finite expectation if

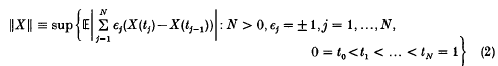
is finite. The function defined by (1), effectively a generalization of the Doléans measure (see e.g. [4] pp. 33–35), is extendible to a bona fide complex measure on Ω × [0, 1] if and only if its ‘total variation’

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 103 , Issue 2 , March 1988 , pp. 367 - 370
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Blei, R. C.. Multi-linear measure theory and multiple stochastic integration.Google Scholar
[2]Blei, R. C.. α-Chaos. J. Funct. Anal., to appear.Google Scholar
[3]Blei, R. C. and Körner, T. W.. Combinatorial dimension and random sets. Israel J. of Math. 47 (1984), 65–74.CrossRefGoogle Scholar
[4]Chung, K. L. and Williams, R. J.. Introduction to Stochastic Integration (Birkhauser-Verlag, 1983).CrossRefGoogle Scholar
[5]Littlewood, J. E.. On bounded bilinear forms in an infinite number of variables. Quart. J. Math. Oxford 1 (1930), 164–174.CrossRefGoogle Scholar