No CrossRef data available.
Complexes of Conics and the Weddle Surface
Published online by Cambridge University Press: 24 October 2008
Extract
A complex or system ∞3 of conics in space of four dimensions is such that a finite number of conics pass through an arbitrary point. Linear complexes are those for which this number is unity, and are such that their curves are defined by conditions of incidence with fixed surfaces, curves and points. In this paper are discussed briefly the linear complexes defined by the condition that their curves meet an irreducible curve in four points. Denoting by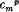 
a curve of order m and genus p it is found that the curves in question are 
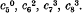The complex associated with 
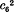is considered in greater detail, since it is found to have an interesting connection with the well-known Weddle quartic surface of ordinary space. In fact the conics of the system touching a space (of three dimensions) do so in the points of such a surface. The main properties of this surface can be thence deduced. In addition we discuss certain results in connection with this curve 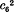. The paper closes with certain enumerative results which were obtained in the course of the researches giving the results recorded and which we believe are worth record.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 3 , 20 September 1924 , pp. 201 - 216
- Copyright
- Copyright © Cambridge Philosophical Society 1924
References
* Excluding the complex defined by a cubic curve on the scroll for which the pencil of conies in each plane have double contact with the conic on the scroll at the points of the cubic curve, and similar cases.
‡ Using these results it can be shown by exhaustion that if a complex is defined by intersections with a set of curves on a cubic scroll these curves taken together form a degenerate curve of one of the four cases, with the exception of the case of the complex defined by four generators, distinct or coincident.
* Salmon-Rogers, , Geometry of three dimensions, ed. 5, vol. 2, § 474.Google Scholar
‡ For example, the method of Picard-Simart, , Fonctions algébraiques de deux variables indépendants…, t. 1, p. 223 (Paris, 1897)Google Scholar shows that it is at least this, and it cannot be greater in the present case, for then six points of an ordinary space would lie on more than ∞3 quadrics.
* ‘Formule di coincidenza per le serie algebriche…,’ Rend. Palermo, 5, 252: (1891)Google Scholar, formula a n−1.
* The representation on the new plane is in fact the representation given by the canonical equations
for the system of conic-planes, and our results can be verified readily by algebraic arguments.
‡ Segre, , “Sull' incidenza di retta e piani…,” Rend. Palermo (1888), p. 45, n. 8.CrossRefGoogle Scholar
* Bertini, , Geometria Proiettiva degli I perspazi, ed. 2 (Messina, 1923), p. 402Google Scholar.
† Jessop, , Quartic Surfaces (Cambridge, 1916), p. 133et seq.Google Scholar
* It may be noted that 
is the locus of points from which is projected into a sextic curve of genus two, having one actual node and lying on a quadric. From a point on the directrix it is projected into a sextic with two actual nodes (h = 6).
* Jessop, , Quartic Surfaces (Cambridge, 1916), p. 173.Google Scholar
† A similar result is: For an ∞2 of quadric forms in [4], the base being a 
its 3-secant, etc., there exist ∞2 planes, the quadrisecant planes, on each of which the system determines a pencil of conics only. 10 such planes pass through a point and 30 meet a fixed plane in lines (§ 9).
* Quoted from Severi, , “Sopra alcune singolarità delle curve di un iperspazio,” Mem. Torino, Ser. 2, t. 51 (1902), p. 81;Google Scholar § 9, n. 22, p. 107.
† In § 9 the symbol 
denotes a curve of order n and rank R, n and R being the variables of the functional relations. The curves are supposed to be general.
* Generally in space of m dimensions the number of [m − 2], m-secant to a 
and meeting a [m − 2] in a [m − 3], is 
* In number 
See Severi, loc. cit., § 8.
* Severi, loc. cit., § 10.