No CrossRef data available.
Published online by Cambridge University Press: 11 April 2025
We prove new statistical results about the distribution of the cokernel of a random integral matrix with a concentrated residue. Given a prime p and a positive integer n, consider a random 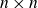 $n \times n$ matrix
$n \times n$ matrix 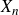 $X_n$ over the ring
$X_n$ over the ring 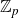 $\mathbb{Z}_p$ of p-adic integers whose entries are independent. Previously, Wood showed that as long as each entry of
$\mathbb{Z}_p$ of p-adic integers whose entries are independent. Previously, Wood showed that as long as each entry of 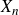 $X_n$ is not too concentrated on a single residue modulo p, regardless of its distribution, the distribution of the cokernel
$X_n$ is not too concentrated on a single residue modulo p, regardless of its distribution, the distribution of the cokernel 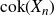 $\mathrm{cok}(X_n)$ of
$\mathrm{cok}(X_n)$ of 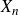 $X_n$, up to isomorphism, weakly converges to the Cohen–Lenstra distribution, as
$X_n$, up to isomorphism, weakly converges to the Cohen–Lenstra distribution, as 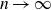 $n \rightarrow \infty$. Here on the contrary, we consider the case when
$n \rightarrow \infty$. Here on the contrary, we consider the case when 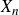 $X_n$ has a concentrated residue
$X_n$ has a concentrated residue 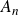 $A_n$ so that
$A_n$ so that 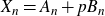 $X_n = A_n + pB_n$. When
$X_n = A_n + pB_n$. When  $B_n$ is a Haar-random
$B_n$ is a Haar-random 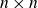 $n \times n$ matrix over
$n \times n$ matrix over 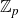 $\mathbb{Z}_p$, we explicitly compute the distribution of
$\mathbb{Z}_p$, we explicitly compute the distribution of 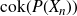 $\mathrm{cok}(P(X_n))$ for every fixed n and a non-constant monic polynomial
$\mathrm{cok}(P(X_n))$ for every fixed n and a non-constant monic polynomial 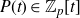 $P(t) \in \mathbb{Z}_p[t]$. We deduce our result from an interesting equidistribution result for matrices over
$P(t) \in \mathbb{Z}_p[t]$. We deduce our result from an interesting equidistribution result for matrices over  $\mathbb{Z}_p[t]/(P(t))$, which we prove by establishing a version of the Weierstrass preparation theorem for the noncommutative ring
$\mathbb{Z}_p[t]/(P(t))$, which we prove by establishing a version of the Weierstrass preparation theorem for the noncommutative ring 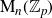 $\mathrm{M}_n(\mathbb{Z}_p)$ of
$\mathrm{M}_n(\mathbb{Z}_p)$ of 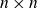 $n \times n$ matrices over
$n \times n$ matrices over 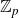 $\mathbb{Z}_p$. We also show through cases the subtlety of the “universality” behavior when
$\mathbb{Z}_p$. We also show through cases the subtlety of the “universality” behavior when 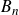 $B_n$ is not Haar-random.
$B_n$ is not Haar-random.