Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T13:56:55.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of certain multivariate distributions*

Published online by Cambridge University Press:  24 October 2008

Y. H. Wang
Y. H. Wang
Affiliation:
Department of Mathematics, Sir George Williams University, Montreal 107, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

Let X1, X2, …, Xn, be n (n ≥ 2) independent observations on a one-dimensional random variable X with distribution function F. Let

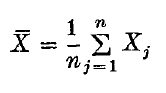
be the sample mean and

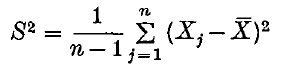
be the sample variance. In 1925, Fisher (2) showed that if the distribution function F is normal then 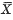and S2 are stochastically independent. This property was used to derive the student's t-distribution which has played a very important role in statistics. In 1936, Geary(3) proved that the independence of 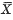and S2 is a sufficient condition for F to be a normal distribution under the assumption that F has moments of all order. Later, Lukacs (14) proved this result assuming only the existence of the second moment of F. The assumption of the existence of moments of F was subsequently dropped in the proofs given by Kawata and Sakamoto (7) and by Zinger (27). Thus the independence of 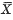and S2 is a characterizing property of the normal distribution.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 75 , Issue 2 , March 1974 , pp. 219 - 234
Copyright
Copyright © Cambridge Philosophical Society 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Anderson, T. W.An Introduction to Multivariate Statistical Analysis (John Wiley and Sons; New York, 1958).Google Scholar
(2)Fisher, R. A.Applications of ‘Student's’ distribution. Metron 5 (1925), 90–104.Google Scholar
(3)Geary, R. C.Distribution of ‘Student's’ ratio for non-normal samples. J. Roy. Statist. Soc. Suppl., Ser. B3 (1936), 178–184.CrossRefGoogle Scholar
(4)Haight, F. A.Handbook of the Poisson distribution (John Wiley and Sons; New York, 1967).Google Scholar
(5)Johnson, N. L. and Kotz, S.Distributions in statistics – discrete distributions (Houghton Muffin; Boston, 1969).Google Scholar
(6)Johnson, N. L. and Kotz, S.Distributions in statistics – continuous multivariate distributions (John Wiley and Sons; New York, 1972).Google Scholar
(7)Kawata, T. and Sakamoto, H.On the characterization of the normal population by the independence of the sample mean and the sample variance. J. Math. Soc. Japan 1 (1949), 111–115.Google Scholar
(8)Krishnaiah, P. R. and Rao, M. M.Remarks on a multivariate gamma distribution. Amer. Math. Monthly 68 (1961), 342–346.Google Scholar
(9)Krishnamoorthy, A. S.Multivariate binomial and Poisson distributions. Sankhyā (1951), 117–124.Google Scholar
(10)Krishnamoorthy, A. S. and Parthasarty, M.A multivariate gamma type distribution. Ann. Math. Statist. 22 (1951), 549–557.CrossRefGoogle Scholar
(11)Krishnamoorthy, A. S. and Parthasarty, M.Correction to Krishnamoorthy–Parthasarty 1951. Ann. Math. Statist. 31 (1960), 229.CrossRefGoogle Scholar
(12)Laha, R. G.On an extension of Geary's theorem. Biometrika 40 (1953), 228–229.Google Scholar
(13)Loève, M.On sets of probability laws and their limit elements. Univ. Calif. Pub. Stat. 1 (1950), 53–88.Google Scholar
(14)Lukacs, E. Acharacterization of the normal distribution. Ann. Math. Statist. 13 (1942), 91–93.CrossRefGoogle Scholar
(15)Lukacs, E. Characterization of populations by properties of suitable statistics. Proc. Third Berkeley Symposium on Math. Stat. and Prob. (Univ. of Calif. Press, Berkeley) 1956, 195–214.Google Scholar
(16)Lukacs, E. Recent developments in the theory of characteristic functions. Proc. Fourth Berkeley Symposium on Math. Stat. and Prob. (Univ. of Calif. Press, Berkeley) (1960), 307–335.Google Scholar
(17)Lukacs, E. and Lana, R. G.Applications of characteristic functions (Charles Griffin; London, 1964).Google Scholar
(18)Moran, P. A. P. and Vere-Jones, D.The infinite divisibility of multivariate gamma dis tributions. Sankhyā, Series A31 (1969), 191–194.Google Scholar
(19)Pierce, D. A. and Dykstra, R. L.Independence and the normal distribution. The Amer. Stat. 23 (1969), 39.Google Scholar
(20)Shanbhag, D. N.Another characteristic property of the Poisson distribution. Proc. Cambridge Philos. Soc. 68 (1970), 167–169.CrossRefGoogle Scholar
(21)Shanbhag, D. N.Comments on Wang's paper. Proc. Cambridge Philos. Soc. 73 (1973), 473–475.CrossRefGoogle Scholar
(22)Steyn, H. S.On discrete multivariate probability functions. Proc. Koninklijke Nederlandse Akademie van Wetenschappen, Ser. A54 (1951), 23–30.Google Scholar
(23)Steyn, H. S.On approximations for the distributions obtained from multiple events. Proc. Koninklijke Nederlandse Akademie van Wetenschappen, Ser. A66 (1963), 85–96.Google Scholar
(24)Tallis, G. M.The use of a generalized multinomial distribution in the estimation of corre lation in discrete data. J. Roy. Statist. Soc., Ser. B24 (1962), 530–534.Google Scholar
(25)Wang, Y. H. On characterization of some probability distributions and estimations of the parameters of the Pareto distribution. Ph.D. Dissertation, the Ohio State University (1971).Google Scholar
(26)Wang, Y. H.On characterization of certain probability distributions. Proc. Cambridge Philos. Soc. 71 (1972), 347–352.Google Scholar
(27)Zinger, A. A.On independent samples from normal population. Uspehi Mat. Nauk (N.S.), 6.5.45 (1951), 172–175.Google Scholar