Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T14:03:53.398Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of the circle and its applications to Hermitian operators

Published online by Cambridge University Press:  24 October 2008

Béla Bollobás
Béla Bollobás
Affiliation:
University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be a complex normed space and let T be a Hermitian linear operator on X (i.e. the numerical range of T is real). It was proved by Bonsall (see (4); Theorem 10.13) that then

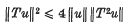
for every u ∈ X. This inequality was improved by the author (3) to

Inequality (1) is closely related (see (3)) to some inequalities of Hadamard (6) and Kolmogorov (7) about the successive derivatives of functions in L∞(−∞, ∞). It was also shown in (3) (and was, in fact, shown already in (7)) that the constant 2 is best possible in (1). However, as we shall see, inequality (1) can be sharpened considerably if T attains its norm on u, i.e. if ‖Tu‖ = ‖T‖‖u‖.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 1 , July 1973 , pp. 69 - 72
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bollob´s, B.The numerical range in Banach algebras and complex functions of exponential type. Bull. London Math. Soc. 3 (1971), 27–33.CrossRefGoogle Scholar
(2)Bollobás, B.A property of Hermitian elements. J. London Math. Soc. 4 (1971), 379–380.Google Scholar
(3)Bollobás, B.Relations between the square and the spatial numerical range of an operator, to appear in J. London Math. Soc.Google Scholar
(4)Bonsall, F. F. and Duncan, J.Numerical ranges of operators on normed spaces and of elements of normed algebras. London Math. Soc. Lecture Notes (Cambridge University Press, 1971).CrossRefGoogle Scholar
(5)Crabb, M. J., Duncan, J. and McGregor, C. M.Some extremal problems in the theory of numerical ranges. Acta Math. 128 (1972), 123–142.CrossRefGoogle Scholar
(6)Hadamard, J.Bull. Soc. Math. France 42, C. R. Séances, 68–72 (1914).Google Scholar
(7)Kolmogorov, A. N.On inequalities between the upper bounds of the successive derivatives of an arbitrary function on an infinite interval. Amer. Math. Soc. Transl. 2 (1962), 233–243.Google Scholar
(8)Levin, B. J. A.Distribution of zeros of entire functions. Amer. Math. Soc. Translations of Math. Monographs, vol. 5 (1964).CrossRefGoogle Scholar
(9)Sinclair, A. M.The norm of a Hermitian element in a Banach Algebra. Proc. Amer. Math. Soc. 28 (1971), 446–450.CrossRefGoogle Scholar