Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T14:42:52.940Z Has data issue: false hasContentIssue false
  • English
  • Français

A centred norm inequality for singular integral operators

Published online by Cambridge University Press:  24 October 2008

Richard F. Bass
Richard F. Bass
Affiliation:
Department of Mathematics, University of Washington, Seattle, Washington 98195, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a standard singular integral kernel on ℝ satisfying the usual Hölder continuity condition of order δ, and define 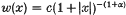(where c is chosen so that the integral of w is 1), 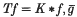the mean of g with respect to the measure w(x) dx, and ‖·‖p the Lp norm with respect to w(x) dx. Although the inequality 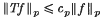is not true in general, the centred norm inequality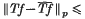 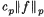does hold for 1 < p < ∞ if α < δ.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 2 , September 1992 , pp. 369 - 383
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bass, R. F.. A probabilistic approach to the boundedness of singular integral operators. In Séminaire de Probabilités XXIV, Lecture Notes in Math. vol. 1426 (Springer-Verlag, 1990), pp. 15–40.Google Scholar
[2]Fefferman, C. and Stein, E. M.. Hp spaces of several variables. Acta Math. 129 (1972), 137–193.CrossRefGoogle Scholar
[3]Stein, E. M.. Singular Integrals and Differentiability Properties of Functions (Princeton University Press, 1970).Google Scholar
[4]Torchinsky, A.. Real-variable Methods in Harmonic Analysis (Academic Press, 1986).Google Scholar