Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T14:52:33.621Z Has data issue: false hasContentIssue false
  • English
  • Français

The central limit theorem for m-dependent variables

Published online by Cambridge University Press:  24 October 2008

P. H. Diananda
P. H. Diananda
Affiliation:
Institute of StatisticsUniversity of North CarolinaChapel Hill, North Carolina*
Get access Rights & Permissions [Opens in a new window]

Extract

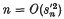In a previous paper (4) central limit theorems were obtained for sequences of m-dependent random variables (r.v.'s) asymptotically stationary to second order, the sufficient conditions being akin to the Lindeberg condition (3). In this paper similar theorems are obtained for sequences of m-dependent r.v.'s with bounded variances and with the property that for large n, where s′n is the standard deviation of the nth partial sum of the sequence. The same basic ideas as in (4) are used, but the proofs have been simplified. The results of this paper are examined in relation to earlier ones of Hoeffding and Robbins(5) and of the author (4). The cases of identically distributed r.v.'s and of vector r.v.'s are mentioned.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 51 , Issue 1 , January 1955 , pp. 92 - 95
Copyright
Copyright © Cambridge Philosophical Society 1955

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cramér, H.Random variables and probability distributions (Cambridge, 1937), pp. 57, 60.Google Scholar
(2)Cramér, H.Mathematical methods of statistics (Princeton, 1946), p. 215.Google Scholar
(3)Diananda, P. H.Some probability limit theorems with statistical applications. Proc. Camb. phil. Soc. 49 (1953), 239–46.CrossRefGoogle Scholar
(4)Diananda, P. H.The central limit theorem for m-dependent variables asymptotically stationary to second order. Proc. Camb. phil. Soc. 50 (1954), 287–92.CrossRefGoogle Scholar
(5)Hoeffding, W. and Robbins, H.The central limit theorem for dependent variables. Duke Math. J. 15 (1948), 773–80.CrossRefGoogle Scholar
(6)Khintchine, A.Asymptotische Gesetze der Wahrscheinlichkeitsrechnung (Berlin, 1933).CrossRefGoogle Scholar