Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T13:48:55.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Carleman's formula for subharmonic functions

Published online by Cambridge University Press:  24 October 2008

C. L. Thompson
C. L. Thompson
Affiliation:
Churchill College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to prove theorems for subharmonic functions analogous to those stated below for regular functions. We make the following definition: D(∈, R) is the domain in the Euclidean plane defined by

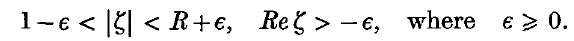
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 51 - 60
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cartwright, M. L.Integral functions (Cambridge, 1956).Google Scholar
(2)Hayman, W. K.Proc. London Math. Soc. (3), 2 (1952), 469–512.CrossRefGoogle Scholar
(3)Hayman, W. K.Comment. Math. Helv. 34 (1960), 75–84.Google Scholar
(4)Itô, J. I.Proc. American Math. Soc. 9 (1958), 763–772.Google Scholar
(5)Kennedy, P. B.Proc. London Math. Soc. (3), 6 (1956), 518–547.CrossRefGoogle Scholar
(6)Rado, T.Subharmonic functions (Berlin, 1937).Google Scholar
(7)Riesz, F.Acta Litt. Szeged 2 (1925).Google Scholar