Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T14:03:29.862Z Has data issue: false hasContentIssue false
  • English
  • Français

A canonical operad pair

Published online by Cambridge University Press:  24 October 2008

Richard Steiner
Richard Steiner
Affiliation:
University of Warwick, Coventry
Get access Rights & Permissions [Opens in a new window]

Extract

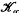The purpose of this paper is to construct an operad ℋ∞ with the good properties of both the little convex bodies partial operad and the little cubes operad 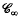used in May's theory of E∞ ring spaces or multiplicative infinite loop spaces ((6), chapter VII). In (6) ℋ can then be used instead of 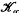and 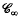, and the theory becomes much simpler; in particular all partial operads can be replaced by genuine ones. The method used here is a modification of that which May suggests on (6), page 170, but cannot carry out.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 3 , November 1979 , pp. 443 - 449
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adams, J. F.Infinite loop spaces. Annals of Mathematics Studies 90 (Princeton University Press; University of Tokyo Press, 1978).CrossRefGoogle Scholar
(2)Cohen, F. R., Lada, T. J. and May, J. P.The homology of iterated loop spaces. Springer Lecture Notes in Mathematics, no. 533 (1976).CrossRefGoogle Scholar
(3)May, J. P.The geometry of iterated loop spaces, Springer Lecture Notes in Mathematics, no. 271 (1972).CrossRefGoogle Scholar
(4)May, J. P.E∞ spaces, group completions, and permutative categories. In New developments in topology, ed. Segal, G. (Cambridge University Press, 1974), pp. 61–93.CrossRefGoogle Scholar
(5)May, J. P.The spectra associated to ℐ-monoids. Math. Proc. Cambridge Philos. Soc. 84 (1978), 313–322.CrossRefGoogle Scholar
(6)May, J. P. (with contributions by F. Quinn N. Ray and J. Tornehave). E ∞ ring spaces and E ∞ ring spectra. Springer Lecture Notes in Mathematics, no. 577 (1977).CrossRefGoogle Scholar
(7)McDuff, D. and Segal, G.omology fibrations and the ‘group completion’ theorem. Invent. Math. 31 (1976), 279–284.CrossRefGoogle Scholar
(8)Segal, G.Configuration-spaces and iterated loop-spaces. Invent. Math. 21 (1973), 213–222.CrossRefGoogle Scholar