Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T13:57:05.482Z Has data issue: false hasContentIssue false
  • English
  • Français

A campanological problem in group theory. II

Published online by Cambridge University Press:  24 October 2008

R. A. Rankin
R. A. Rankin
Affiliation:
University of Glasgow
Get access Rights & Permissions [Opens in a new window]

Extract

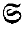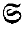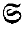1. Let E be a finite non-null set and write (E) for the family of all permutations of E. Let be a non-null subset of (E) and write () for the subgroup of (E) generated by the members of . For any α ∈ we put

so that () is a subgroup of () and is independent of the choice of α in . We suppose that E splits into k disjoint transitivity sets (orbits) Ei(1 ≤ i ≤ k) with respect to (); thus σEi = Ei for all σ ∈ ().

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 11 - 18
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Burns, J.The abstract groups of degree 8. American J. Math. 37 (1915), 195–214.CrossRefGoogle Scholar
(2)Rankin, R. A.A campanological problem in group theory. Proc. Cambridge Philos. Soc. 44 (1948), 17–25.CrossRefGoogle Scholar