Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T09:38:19.648Z Has data issue: false hasContentIssue false
  • English
  • Français

Brandt semigroups of quotients

Published online by Cambridge University Press:  24 October 2008

John Fountain  and
Mario Petrich
John Fountain
Affiliation:
Department of Mathematics, University of York, Heslington, York Y01 5DD and Institut für Mathematik, Universität Wien
Mario Petrich
Affiliation:
Department of Mathematics, University of York, Heslington, York Y01 5DD and Institut für Mathematik, Universität Wien
Get access Rights & Permissions [Opens in a new window]

Extract

In an earlier paper [3], we introduced a new notion of completely 0-simple semigroup of quotients. The definition is motivated by a connection between Artinian simple rings and completely 0-simple semigroups. Given an Artinian simple ring Q, one obtains a completely 0-simple multiplicative sub-semigroup 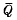by taking the union of the subsets eiQej(i, j = l,…, n), where 1 = e1 + … + en and the ei are primitive orthogonal idempotents. If Q is the classical ring of left quotients of R, then 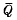is a semigroup of left quotients of 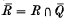in the sense that every element q in 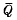can be written as q = a-1b for some elements a, b in 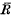with a2 ≠ 0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 3 , November 1985 , pp. 413 - 426
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Clifford, A. H. and Preston, G. B.. The Algebraic Theory of Semigroups, Mathematical Surveys 7, vol. 1 (American Mathematical Society, 1961).Google Scholar
[2]Fountain, J. B.. Abundant semigroups. Proc. London Math. Soc. (2) 44 (1982), 103–129.CrossRefGoogle Scholar
[3]Fountain, J. B. and Petrich, M.. Completely 0-simple semigroups of quotients. J. Algebra, to appear.Google Scholar
[4]Lallement, G. and Petrich, M.. Décompositions I-matricielles d'un demi-groupe. J. Math. Pures Appl. 45 (1966), 67–117.Google Scholar
[5]McAlister, D. B.. One-to-one partial right translations of a right cancellative semigroup. J. Algebra 43 (1976), 231–251.CrossRefGoogle Scholar
[6]Pastijn, F.. A representation of a semigroup by a semigroup of matrices over a group with zero. Semigroup Forum 10 (1975), 238–249.CrossRefGoogle Scholar
[7]Petrich, M.. Introduction to Semigroups (Merrill, 1973).Google Scholar