Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T14:28:07.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Binary integral quadratic forms over R(t)

Published online by Cambridge University Press:  24 October 2008

James T. Knight
James T. Knight
Affiliation:
Trinity College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

We use the notations and definitions of the introduction to the previous paper ((1)), and say that 2 lattices K and L on a quadratic space over R(t) with its Dedekind set C are in the same genus if, for all 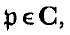, the lattices 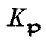and 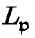are in the same class. We mean to count the number of classes of lattices in a given genus over a binary space: we shall find that it is either 1 or .

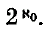Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 3 , July 1966 , pp. 433 - 440
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Knight, J. T.Quadratic forms over R(t). Proc. Cambridge Philos. Soc. 62 (1966), 197–205.CrossRefGoogle Scholar
(2)O'meara, O. T.Introduction to quadratic forms (Springer-Verlag, 1963).CrossRefGoogle Scholar