Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T14:24:30.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Bending of a circular plate with an eccentric circular patch symmetrically loaded with respect to its centre

Published online by Cambridge University Press:  24 October 2008

W. A. Bassali  and
R. H. Dawoud
W. A. Bassali
Affiliation:
Faculty of ScienceAlexandria University
R. H. Dawoud
Affiliation:
Faculty of EngineeringCairo University
Get access Rights & Permissions [Opens in a new window]

Abstract

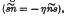The complex variable method is applied to obtain solutions for the deflexion of a supported circular plate with uniform line loading along an eccentric circle under a general boundary condition including the clamped boundary , a boundary with zero peripheral couple 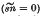, a boundary with equal boundary cross-couples 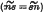, a hinged boundary 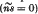and a boundary for which 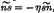, η being Poisson's ratio. These solutions are used to obtain the deflexion at any point of a circular plate having an eccentric circular patch symmetrically loaded with respect to its centre. Expressions for the slope and cross-couples over the boundary and the deflexions at the centres of the plate and the loaded patch are obtained.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 52 , Issue 3 , July 1956 , pp. 584 - 598
Copyright
Copyright © Cambridge Philosophical Society 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Clebsch, A.Theorie der Elastizität fester Körper (Leipzig, 1862).Google Scholar
(2)Dawoud, R. H. Proc. math. phys. Soc. Egypt (in the Press). See also Ph.D. thesis, London, 1950.Google Scholar
(3)Flügge, W.Die strenge Berechnung von Kreisplatten unter Einzellasten (Berlin, 1928).CrossRefGoogle Scholar
(4)Michell, J. H.Proc. Lond. math. Soc. 34 (1901), 223.CrossRefGoogle Scholar
(5)Schmidt, H.Ingen. -Arch. 1 (1930), 147.CrossRefGoogle Scholar
(6)Stevenson, A. C.Phil. Mag. (7), 33 (1942), 639.CrossRefGoogle Scholar
(7)Stevenson, A. C.Phil. Mag. (7), 34 (1943), 105.Google Scholar
(8)Timoshenko, S.Theory of plates and shells (New York, 1940), p. 68.Google Scholar