Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T18:46:55.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphism sequences of free nilpotent groups of class two

Published online by Cambridge University Press:  24 October 2008

Joan L. Dyer  and
Edward Formanek
Joan L. Dyer
Affiliation:
H. H. Lehman College, New York and University of Pisa
Edward Formanek
Affiliation:
H. H. Lehman College, New York and University of Pisa
Get access Rights & Permissions [Opens in a new window]

Extract

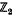In this paper we prove that the automorphism group A(N) of a free nilpotent group N of class 2 and finite rank n is complete, except when n is 1 or 3. Equivalently, the centre of A(N) is trivial and every automorphism of A(N) is inner, provided n ≠ 1 or 3. When n = 3, A(N) has an our automorphism of order 2, so A(A(N)) is a split extension of A(N) by . In this case, A(A(N)) is complete. These results provide some evidence supporting a conjecture of Gilbert Baumslag that the sequence

becomes periodic if N is a finitely generated nilpotent group.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 2 , March 1976 , pp. 271 - 279
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bachmute, S.Induced automorphisme of free groups and free metabelian groups. Tras. Amer. Math. Soc. 122 (1966), 1–17.Google Scholar
(2)Burnside, W.Theory of groups of finite order (Dover, 1955).Google Scholar
(3)Dyer, J. L. and Formanek, E.The automorphism group of a free group is complete. J. London Math. Soc. (2), 10 (1975), to appear.Google Scholar
(4)Hua, L. K. and Reiner, I.Automorphisme of the unimodular group. Trans. Amer. Math. Soc. 71 (1951), 331–348.Google Scholar
(5)Magnus, W., Karrass, S. A. and Solitar, D.Combinatorial group theory (Wiley; Interscience, 1966).Google Scholar