Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T08:12:38.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Augmented base loci and restricted volumes on normal varieties, II: The case of real divisors

Published online by Cambridge University Press:  12 October 2015

ANGELO FELICE LOPEZ
ANGELO FELICE LOPEZ*
Affiliation:
Dipartimento di Matematica e Fisica, Università di Roma Tre, Largo San Leonardo Murialdo 1, 00146, Roma, Italy. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a normal projective variety defined over an algebraically closed field and let Z be a subvariety. Let D be an 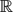${\mathbb R}$-Cartier 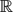${\mathbb R}$-divisor on X. Given an expression (*) D$\sim_{\mathbb R}$t1H1 +. . .+ tsHs with ti ∈ 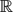${\mathbb R}$ and Hi very ample, we define the (*)-restricted volume of D to Z and we show that it coincides with the usual restricted volume when Z$\not\subseteq$B+(D). Then, using some recent results of Birkar [Bir], we generalise to 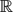${\mathbb R}$-divisors the two main results of [BCL]: The first, proved for smooth complex projective varieties by Ein, Lazarsfeld, Mustaţă, Nakamaye and Popa, is the characterisation of B+(D) as the union of subvarieties on which the (*)-restricted volume vanishes; the second is that X − B+(D) is the largest open subset on which the Kodaira map defined by large and divisible (*)-multiples of D is an isomorphism.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 3 , November 2015 , pp. 517 - 527
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BBP] Boucksom, S., Broustet, A. and Pacienza, G. Uniruledness of stable base loci of adjoint linear systems via Mori theory. Math. Z. 275 (2013), no. 1–2, 499–507.Google Scholar
[BCHM] Birkar, C., Cascini, P., Hacon, C. and McKernan, J. Existence of minimal models for varieties of log general type. J. Amer. Math. Soc. 23 (2010), no. 2, 405–468.Google Scholar
[BCL] Boucksom, S., Cacciola, S. and Lopez, A. F. Augmented base loci and restricted volumes on normal varieties. Math. Z. 278 (2014), no. 3–4, 979–985.Google Scholar
[BDPP] Boucksom, S., Demailly, J. P., Păun, M. and Peternell, T. The pseudo-effective cone of a compact Kähler manifold and varieties of negative Kodaira dimension. J. Algebraic Geom. 22 (2013), no. 2, 201–248.Google Scholar
[Bir] Birkar, C. The augmented base locus of real divisors over arbitrary fields. Preprint (2013) arXiv:1312.0239.Google Scholar
[Bou] Boucksom, S. Corps d'Okounkov (d'après Okounkov, Lazarsfeld–Mustaţă and Kaveh–Khovanskii). Séminaire Bourbaki. vol. 2012/2013, exposé 1059. Preprint available at http://www.math.jussieu.fr/~boucksom/publis.html.Google Scholar
[DP] Di Biagio, L. and Pacienza, G. Restricted volumes of effective divisors. Preprint (2012) arXiv:1207.1204Google Scholar
[ELMNP1] Ein, L., Lazarsfeld, R., Mustaţă, M., Nakamaye, M. and Popa, M. Asymptotic invariants of base loci. Ann. Inst. Fourier (Grenoble) 56 (2006), no. 6, 1701–1734.Google Scholar
[ELMNP2] Ein, L., Lazarsfeld, R., Mustaţă, M., Nakamaye, M. and Popa, M. Restricted volumes and base loci of linear series. Amer. J. Math. 131 (2009), no. 3, 607–651.Google Scholar
[HM] Hacon, C. D. and McKernan, J. Boundedness of pluricanonical maps of varieties of general type. Invent. Math. 166 (2006), no. 1, 1–25.Google Scholar
[Laz] Lazarsfeld, R. Positivity in algebraic geometry, I. Ergeb. Math. Grenzgeb 3. Folge 48 (Springer-Verlag, Berlin, 2004.)Google Scholar
[Leh] Lehmann, B. Comparing numerical dimensions. Algebra Number Theory 7 (2013), no. 5, 1065–1100.Google Scholar
[N] Nakamaye, M. Stable base loci of linear series. Math. Ann. 318 (2000), no. 4, 837–847.Google Scholar
[T] Takayama, S. Pluricanonical systems on algebraic varieties of general type. Invent. Math. 165 (2006), no. 3, 551–587.Google Scholar
[Z] Zariski, O. The theorem of Riemann-Roch for high multiples of an effective divisor on an algebraic surface. Ann. of Math. (2) 76 (1962), 560–615.Google Scholar