Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-30T21:00:19.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Artin's primitive root conjecture and a problem of Rohrlich

Published online by Cambridge University Press:  01 May 2014

CHRISTOPHER AMBROSE
CHRISTOPHER AMBROSE*
Affiliation:
Mathematisches Institut, Georg-August-Universität Göttingen, Bunsenstraße 3–5, 37073 Göttingen, Deutschland. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 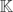$\mathbb{K}$ be a number field, Γ a finitely generated subgroup of 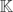$\mathbb{K}$*, for instance the unit group of 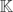$\mathbb{K}$, and κ>0. For an ideal $\mathfrak{a}$ of 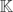$\mathbb{K}$ let indΓ($\mathfrak{a}$]></alt-text></inline-graphic>) denote the multiplicative index of the reduction of Γ in <inline-graphic name="S0305004114000206_inline3"><alt-text><![CDATA[$(\mathcal{O}_\mathbb{K}/\mathfrak{a})$* (whenever it makes sense). 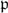For a prime ideal $\mathfrak{p}$ of 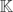$\mathbb{K}$ and a positive integer γ let 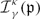$\mathcal{I}_\gamma^\kappa(\mathfrak{p})$ be the average of 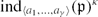${ind}_{\langle a_1,\dots,a_\gamma\rangle}(\mathfrak{p})^\kappa$ over all tupels 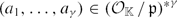$(a_1,\dots,a_\gamma)\in{(\mathcal{O}_\mathbb{K}/\mathfrak{p})^*}^\gamma$. Motivated by a problem of Rohrlich we prove, partly conditionally on fairly standard hypotheses, lower bounds for 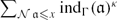$\sum_{\mathcal{N}{\mathfrak{a}\leq x}{ind}_{\Gamma}({\mathfrak{a})^\kappa$ and asymptotic formulae for 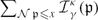$\sum_{\mathcal{N}\mathfrak{p} \leq x} {\mathcal{I}_{\gamma}^\kappa({\mathfrak{p})$.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 157 , Issue 1 , July 2014 , pp. 79 - 99
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, R. C. and Harman, G.Shifted primes without large prime factors. Acta Arith. 83 (1998), pp. 331–361.Google Scholar
[2]Balog, A.p+a without large prime factors. In Seminar on Number Theory, 1983–1984 (Talence, 1983/1984); (Université Bordeaux I, Talence, 1984), pp. Exp. No. 31, 5.Google Scholar
[3]Blomer, V. and Brumley, F.On the Ramanujan conjecture over number fields. Ann. of Math. (2); 174 (2011), pp. 581–605.CrossRefGoogle Scholar
[4]Bombieri, E., Friedlander, J. B. and Iwaniec, H.Primes in arithmetic progressions to large moduli. III. J. Amer. Math. Soc. 2 (1989), pp. 215–224.CrossRefGoogle Scholar
[5]Erdős, P. and Murty, M. R.On the order of a mod p, In Number Theory (Ottawa, ON, 1996). CRM Proc. Lecture Notes vol. 19 (Amer. Math. Soc. Providence, RI, 1999), pp. 87–97.Google Scholar
[6]Felix, A. T.Generalizing the Titchmarsh divisor problem. Int. J. Number Theory 8 (2012), pp. 613–629.Google Scholar
[7]Friedlander, J. and Iwaniec, H.Opera de Cribro. American Mathematical Society Colloquium Publications vol. 57. (American Mathematical Society, Providence, RI, 2010).Google Scholar
[8]Friedlander, J. B.Shifted primes without large prime factors. In Number Theory and Applications (Banff, AB, 1988). NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. vol. 265. (Kluwer Academic Published, Dordrecht, 1989), pp. 393–401.Google Scholar
[9]Hilbert, D.The Theory of Algebraic Number Fields (Springer-Verlag, Berlin, 1998).Google Scholar
[10]Jantzen, J. C. and Schwermer, J.Algebra (Springer-Verlag, Berlin, 2009).Google Scholar
[11]Kim, H. H.Functoriality for the exterior square of GL4 and the symmetric fourth of GL2. J. Amer. Math. Soc. 16 (2003), pp. 139–183 (electronic). With Appendix 1 by Dinakar Ramakrishnan and Appendix 2 by Kim and Peter Sarnak.Google Scholar
[12]Kurlberg, P.On the order of unimodular matrices modulo integers. Acta Arith. 110 (2003), pp. 141–151.CrossRefGoogle Scholar
[13]Kurlberg, P. and Pomerance, C.On a problem of Arnold: the average multiplicative order of a given integer, Algebra Number Theory 7 (2013), pp. 981–999.CrossRefGoogle Scholar
[14]Lagarias, J. C. and Odlyzko, A. M.Effective versions of the Chebotarev density theorem. Algebraic Number Fields: L-functions and Galois Properties (Proc. Sympos., Univ. Durham, Durham, 1975) (Academic Press, London, 1977) pp. 409–464.Google Scholar
[15]Lenstra, H. W. Jr., On Artin's conjecture and Euclid's algorithm in global fields. Invent. Math. 42 (1977), pp. 201–224.Google Scholar
[16]Linnik, J. V.The Dispersion Method in Binary Additive Problems. Trans. by Schuur, S. (American Mathematical Society, Providence, R.I., 1963).Google Scholar
[17]Lorenz, F.Algebraische Zahlentheorie (Bibliographisches Institut, Mannheim 1993).Google Scholar
[18]Luca, F. and Sankaranarayanan, A.On the moments of the Carmichael λ function. Acta Arith. 123 (2006), pp. 389–398.Google Scholar
[19]Luo, W., Rudnick, Z. and Sarnak, P.On the generalized Ramanujan conjecture for GL(n). In Automorphic Forms, Automorphic Representations and Arithmetic (Fort Worth, TX, 1996). Proc. Sympos. Pure Math. vol. 66. (Amer. Math. Soc. Providence, RI, 1999) pp. 301–310.CrossRefGoogle Scholar
[20]Murty, M. R. and Murty, V. K.A variant of the Bombieri–Vinogradov theorem. In Number Theory (Montreal, Que., 1985). CMS Conf. Proc. vol. 7 (Amer. Math. Soc. Providence, RI, 1987), pp. 243–272.Google Scholar
[21]Murty, M. R. and Petersen, K.A Bombieri–Vinogradov theorem for all number fields, Trans. Amer. Math. Soc. 365 (2013), pp. 4987–5032.Google Scholar
[22]Narkiewicz, W.Elementary and Analytic Theory of Algebraic Numbers. Springer Monogr. Math. (Springer-Verlag, Berlin, third ed., 2004).Google Scholar
[23]Neukirch, J.Algebraische Zahlentheorie (Springer-Verlag, Berlin, 2007).Google Scholar
[24]Rohrlich, D. E.Self-dual Artin representations. In Automorphic Representations and L-functions, vol. 22 (Tata Institute of Fundamental Research Studies in Mathematics, Mumbai, 2013), pp. 455–499.Google Scholar
[25]Rohrlich, D. E.Nonvanishing of L-functions for GL(2). Invent. Math. 97 (1989), pp. 381–403.Google Scholar
[26]Serre, J.-P. Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. (1981), pp. 323–401.Google Scholar
[27]Stark, H. M.Some effective cases of the Brauer–Siegel theorem. Invent. Math. 23 (1974), pp. 135–152.Google Scholar
[28]Tenenbaum, G.Introduction to Analytic and Probabilistic Number Theory. Cambridge Studies in Advanced Math. vol. 46. (Cambridge University Press, Cambridge, 1995).Google Scholar
[29]Wagstaff, S. S. Jr., Pseudoprimes and a generalization of Artin's conjecture. Acta Arith. 41, pp. 141–150.CrossRefGoogle Scholar
[30]Washington, L. C.Introduction to Cyclotomic Fields. Graduate Texts in Math. vol. 83. (Springer-Verlag, New York, second ed., 1997).Google Scholar
[31]Zelinsky, J. Upper bounds for the number of primitive ray class characters with conductor below a given bound. arXiv:1307.2319 [math.NT].Google Scholar