No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let R denote a commutative Noetherian ring with an identity element and N a finitely generated R -module. When K is a submodule of N and A an ideal of R the Artin–Rees lemma states that there is an integer q ≥ 0 such that AnN ∩ K = An−q(AqN ∩ K) for all n ≥ q (Rees[4]; Northcott [3], theorem 20, p. 210; Atiyah and Macdonald [1], proposition 10·9, p. 107; Nagata [2], theorem (3·7), p. 9). The above equation belongs to the family of module equations involving A and K which is considered below. We characterize, in terms of A and K, the set of submodules X of N for which there is an integer q = q(X) ≥ 0 satisfying the equation
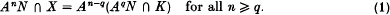
Equation (1), which we call the Artin–Rees equation related to A and K, gets its maximal force when X is largest and we determine the best possible solution in this sense. Notice that for any submodule X satisfying (1), X ⊆ K:NAn for all n ≥ q(X). Since N is a Noetherian R-module ([3], proposition 1 (corollary), p. 177), there is an integer t ≥ 1 such that K:NAt = K:NAt+n for all n ≥ 0. We define M = K:NAt and prove, in Theorem 1, that X = Q satisfies equation (1), for a suitable integer q(Q) ≥ 0, if and only if K ⊆ Q:NAυ ⊆ M for some integer υ ≥ 0. In topological terms, the A-adic topology of K coincides with the topology induced by the A-adic topology of N on the subspace Q if the inequality K ⊆ Q:NAυ ⊆ M is satisfied. It follows that the solution set of equation (1) includes every submodule of N of the form An−rK when n ≥ r = q(K) as well as every submodule lying between K and M. Hence, X = M is the strongest solution, in the sense that M is the largest such submodule contained in An−s (AsN ∩ K): NAn for all n ≥ s = q(M). Recall that M is strictly larger than K if and only if A is contained in at least one prime ideal of R belonging to K ([3], theorem 14 (corollary 1), p. 193). Thus, equation (1) has a unique solution (necessarily X = K) if and only if A is not contained in any prime ideal of R belonging to any solution.