Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T14:41:53.291Z Has data issue: false hasContentIssue false
  • English
  • Français

The arithmetic plurigenera of surfaces

Published online by Cambridge University Press:  24 October 2008

P. M. H. Wilson
P. M. H. Wilson
Affiliation:
Jesus College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let S0 be a complex projective surface with only isolated Gorenstein singularities (see Introduction to (12)). By Serre's criterion ((4), p. 185) this is equivalent to saying that S0 is normal and Gorenstein. By an algebraic smooth deformation of S0, we shall mean a flat, proper morphism of varieties, ρ: 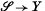say, with fibre ρ−1(y0) = S0 for some y0 ∈ Y and with the general fibre ρ−1(y) = S being a smooth surface. In the paper (12), we studied such smooth deformations of S0 and in particular the behaviour of the plurigenera Pn of the surfaces in the family. The main result of (12) was the fact that Pn(S0) ≤ Pn(S) for all positive integers n, where the choice of the particular smooth surface was irrelevant by a result of Iitaka(5). To prove the above result we introduced what were called the arithmetic plurigenera of S0, which we define again below. In this paper we shall study more closely these arithmetic quantities, and in the process answer some of the questions posed in (11).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 1 , January 1979 , pp. 25 - 31
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Artin, M.Some numerical criteria for contractability of curves on algebraic surfaces. Amer. J. Math. 84 (1962), 485–496.CrossRefGoogle Scholar
(2)Bombieri, E. and Husemoller, D.Classification and embeddings of surfaces. In Algebraic geometry, Arcata 1974. Amer. Math. Soc. Proc. Symp. Pure Math. 29 (1975), 329–420.CrossRefGoogle Scholar
(3)Grothendieck, A. and Dieudonne, J.Eléments de géométrie algébrique: II. Publ. Math. IHES 11 (1961).Google Scholar
(4)Hartshorne, R.Algebraic geometry. Graduate Texts in Mathematics, no. 52 (Springer-Verlag, 1977).CrossRefGoogle Scholar
(5)Iitaka, S.Deformations of compact complex surfaces: II. J. Math. Soc. Japan 22 (1970), 247–261.Google Scholar
(6)Iitaka, S.On D-dimensions of algebraic varieties. J. Math. Soc. Japan 23 (1971), 356–373.CrossRefGoogle Scholar
(7)Kodaira, K.On compact analytic surfaces: II. Ann. of Math. 77 (1963), 563–626.CrossRefGoogle Scholar
(8)Nagata, M.On automorphism group of k[x, y]. Lectures in Mathematics 5, Kyoto University (Kinokuniya Book-Store, Tokyo, 1972).Google Scholar
(9)Serre, J.-P.Géométrie algébrique et géométrie analytique. Ann. Inst. Fourier 6 (1956), 1–42.CrossRefGoogle Scholar
(10)Ueno, K.Classification theory of algebraic varieties and compact complex spaces. Lecture Notes in Mathematics, no. 439 (Springer-Verlag, 1975).CrossRefGoogle Scholar
(11)Wilson, P. M. H. The degeneration of surfaces in an algebraic family. Ph.D. Thesis, University of Cambridge, 1977.Google Scholar
(12)Wilson, P. M. H.The behaviour of the plurigenera of surfaces under algebraic smooth deformations. Inventiones Math. 47 (1978), 289–299.CrossRefGoogle Scholar
(13)Zariski, O.The theorem of Riemann-Roch for high multiples of an effective divisor on an algebraic surface. Ann. of Math. 76 (1962), 560–615.CrossRefGoogle Scholar