Applications of lattice algebra
Published online by Cambridge University Press: 24 October 2008
Extract
By a finite lattice† is meant any finite class 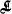 having the following properties:
having the following properties:
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 30 , Issue 2 , 30 April 1934 , pp. 115 - 122
- Copyright
- Copyright © Cambridge Philosophical Society 1934
References
† The terminology and symbols of this paper are borrowed wholesale from the author's article “On the combination of subalgebras”, Proc. Camb. Phil. Soc. 29 (1933), 441–464Google Scholar. This will be referred to as “Subalgebras” in later footnotes.
‡ “Subalgebras”, Theorem 10·2, condition (2). By A > B is meant A ⊃ B but A ≠ B.
§ “Subalgebras”, Corollary 6·4.
† This result was found by R. Dedekiud, Gesammelte Werke, Braunschweig, 1931, Vol. ii. p. 115.
‡ “Subalgebras”, Theorem 4·1.
† “Subalgebras”, Tables I—III.
‡ “Subalgebras”, Theorem 4·1.
§ By the phrase ‘A covers B’ is meant A > B, while A > X > B has no solution. L evidently exists (“Subalgebras”, Theorem 7·1).
† “Subalgebras”, p. 446, § 9.
‡ “Subalgebras”, Theorem 10·2.
§ There are really six conditions, because of the symmetry between join and meet, which ascribes to (1)—(3) symmetric counterparts.
∥ Condition (1) can be very considerably weakened. Reference to (2) and VI* permits us to replace ‘A ⊂ C’ by ‘A is covered by C', and ‘A ∩ (X, C) = (A ∩ X, C)’ by ‘A ∩ (X, C) ⊃ (A ∩ X, C)’ in the first half, to qualify the second half by demanding that A, B, and C shall all cover the same element E, and to replace the equality by an inequality.
† “Subalgebras”, Theorem 26·1.
‡ “Subalgebras”, Theorem 25·2.
§ Cf. Remak, R., “Über minimale invariante Untergruppen, etc.”, Journ. f. Math. 162 (1930), 1–16.Google Scholar
∥ More precisely, be (1, 1) isomorphic in the sense of van der Waerden, , Moderne Algebra (Berlin, 1930–1931), 1, pp. 28–9.CrossRefGoogle Scholar
¶ Since coherent normal subgroups are Abelian; see R. Remak, op. cit., Theorem 2.
† “Subalgebras”, Theorem 17·4.
‡ “Subalgebras”, p. 460.
- 10
- Cited by


