Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T21:42:21.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Analogue of a theorem of Khintchine in fields of formal power series

Published online by Cambridge University Press:  24 October 2008

T. W. Cusick
T. W. Cusick
Affiliation:
Churchill College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

For a real number λ, ‖λ‖ is the absolute value of the difference between λ and the nearest integer. Let X represent the m-tuple (x1, x2, … xm) and let

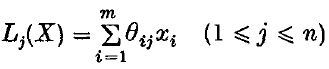
be any n linear forms in m variables, where the Θij are real numbers. The following is a classical result of Khintchine (1):

For all pairs of positive integers m, n there is a positive constant Г(m, n) with the property that for any forms Lj(X) there exist real numbers α1, α2, …, αn such that

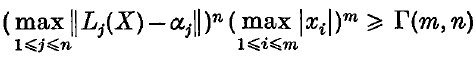
for all integers x1, x2, …, xm not all zero.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 4 , October 1966 , pp. 637 - 642
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Khintchine, Y. A.Über eine Klasse linear Diophantischer Approximationen. Bend. Circ. Mat. Palermo 50 (1926), 170–195.CrossRefGoogle Scholar
(2)Aggarwal, S. K.Analogue of a theorem of Khintchine in a field of formal Laurent series (Abstract 65T-357). Notices Amer. Math. Soc. 12 (1965), 620.Google Scholar
(3)Cassels, J. W. S.An introduction to diophantine approximation, pp. 85–90 (Cambridge, 1957).Google Scholar
(4)Mahler, K.An analogue to Minkowski's geometry of numbers in a field of series. Ann. of Math. 42 (1941), 488–522.CrossRefGoogle Scholar