No CrossRef data available.
An Involution in the Complex Variable
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose that ƒ1, ƒ2, ƒ3 are three quadratics in the complex variable z with complex coefficients, say
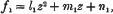
and consider the equation
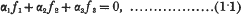
the α's being real quantities. It determines two values ζ, ζ′ of z and thus two points P, P′ in the complex plane. Clearly when P is given the ratios α1: α2: α3 are in general determinate and accordingly P′ also. This is the involutory transformation I propose to discuss.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 24 , Issue 2 , April 1928 , pp. 210 - 217
- Copyright
- Copyright © Cambridge Philosophical Society 1928
References
* The disadvantage is natural to the method. Complex variable geometry is tantamount to geometry on a quadric surface, the position of a point being fixed by the parameters z, 
(now quite independent quantities) of the generators through it. §1 would thus open with two sets of quadratics, one in z, the other in ; the quantities a would be thesame for both. Logically there is a gain and there is a loss of flexibility.Google Scholar
* In the original form P, P′ are the real foci of a member of a net of curves of class three, all of which touch the line at infinity. The reduction corresponds exactly to that of the case of conics given above.Google Scholar
* Clifford, , Collected Papers, pp. 38–54.Google Scholar
* Cf. Baker, , Principles of Geometry, vol. III. p. 42.Google Scholar
* I rely on the simple construction for the inverse of a point P in a circle. Suppose that PI, PJ cut the circle again in G, H; then IH and JG meet in the inverse. Similarly for the image of P in a straight line.Google Scholar
* Proc. Camb. Phil. Soc. vol. XXIII. p. 850.Google Scholar