Article contents
An interpretation of negative probabilities
Published online by Cambridge University Press: 24 October 2008
Extract
1. Let (S, S,μ) be a measure-space, and let f(x) and ø(x) be two μ-integrable functions defined in S. We shall assume that f(x) is a ‘difficult’ function, of which all that is known is how to calculate f(x), generally by a rather complicated process, for any given x∈S; and that ø(x) is an ‘easy’ function, whose value for any x, and whose integral over any subset T of S belonging to the class S of μ-measurable sets, are relatively simple to obtain. We shall define the sets
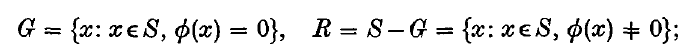
and assume that
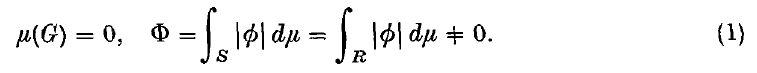
It will be of interest to consider those functions ø(x) which may be regarded as approximations to f(x) in S.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 83 - 86
- Copyright
- Copyright © Cambridge Philosophical Society 1966
- 6
- Cited by


