Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T23:31:53.140Z Has data issue: false hasContentIssue false
  • English
  • Français

An inner measure associated with a von Neumann algebra

Published online by Cambridge University Press:  24 October 2008

G. de Barra
G. de Barra
Affiliation:
Royal Holloway College
Get access Rights & Permissions [Opens in a new window]

Extract

An ‘inner measure’ analogous to Lebesgue inner measure and associated with a von Neumann algebra 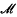is constructed on the linear sets of a Hilbert space. We supposed 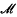to be of finite type and countably decomposable, as these restrictions will be necessary for some of the results obtained. As remarked by Dye in (2), Type II1 algebras have a structure analogous to that of a finite non-atomic measure space, the trace corresponding to the measure. We define a class of ‘measurable sets’ and obtain some of its properties. The development of the theory is indicated also from the starting point of a function-valued dimension function. The idea for the construction of such an inner measure comes from a remark in (3), paragraph 16·2, and the terminology of (3) and of (5) is used throughout.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 3 , July 1968 , pp. 645 - 650
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Dixmier, J.Les algèbras d'opérateurs dans l'espace Hilbertien (Gauthier-Villars, Paris, 1957).Google Scholar
(2)Dye, H. A.The unitary structure in finite rings of operators. Duke Math. J. 20 (1953), 55–69.CrossRefGoogle Scholar
(3)Murray, F. J.and Neumann Von J. On rings of operators. Ann. of Math. 37 (1936), 116–229.CrossRefGoogle Scholar
(4)Sankaran, S.Stochastic convergence for operators. Quart. J. Math., Oxford (2) 15 (1964), 97–102.CrossRefGoogle Scholar
(5)Segal, I. E.A non-commutative extension of abstract integration. Ann. of Math. 57 (1953), 401–457.CrossRefGoogle Scholar
(6)Stinespring, W. F.Integration theorems for gates and duality for unimodular groups. Trans. Amer. Math. Soc. 90 (1959), 15–56.CrossRefGoogle Scholar