Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T11:33:35.435Z Has data issue: false hasContentIssue false
  • English
  • Français

An inequality involving Radon-Nikodym derivatives

Published online by Cambridge University Press:  24 October 2008

J. F. C. Kingman
J. F. C. Kingman
Affiliation:
University of Sussex
Get access Rights & Permissions [Opens in a new window]

Extract

In (2) a simple proof was given of the following inequality of Atkinson, Watterson and Moran (l), a slight generalization of a result of Scheuer and Mandel ((4), see also (3)) which is of importance in genetics. If aij, pi, qj (i, j = 1, 2, 3,…) are non-negative numbers with

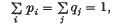
and if

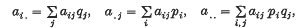
then

and if then This result is shown in (2) to be a special case of a large class of inequalities involving sets of non-negative numbers depending on several indices, and ‘partial averages’ over subsets of those indices.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 1 , January 1967 , pp. 195 - 198
Copyright
Copyright © Cambridge Philosophical Society 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Atkinson, F. V., Watterson, G. A. and Moran, P. A. P.A matrix inequality. Quart. J. Math. (Oxford) (2), 11 (1960), 137–140.CrossRefGoogle Scholar
(2)Kingman, J. F. C.On an inequality in partial averages. Quart. J. Math. (Oxford) (2), 12 (1961), 78–80.CrossRefGoogle Scholar
(3)Mulholland, H. P. and Smith, C. A. B.An inequality arising in genetical theory. Amer. Math. Monthly 66 (1959), 673–683.CrossRefGoogle Scholar
(4)Scheuer, P. A. G. and Mandel, S. P. H.An inequality in population genetics, Heredity 13 (1959), 519–524.CrossRefGoogle Scholar