No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
It has been shown by Kulakoff that if G is a group, not cyclic, of order pl, p being an odd prime, the number of subgroups of G of order pk, for 0 < k < l, is congruent to 1 + p (mod p2); and by Hall that if G is any group of finite order whose Sylow subgroups of G of order pk, p being odd, are not cyclic, then, for 0 < k < l, the number of subgroups of G of order pk is congruent to 1 + p (mod p2). No results were given for the case p = 2. In the present paper it is shown that analogous results hold for the case p = 2, but that the role of the cyclic groups is played by groups of four exceptional types: the cyclic groups themselves, and three non-Abelian types. These groups are defined as follows:
(1) The dihedral group, of order 2k, generated by A and B, where
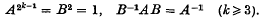
(2) The quaternion group, of order 2k, generated by A and B, where
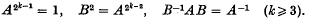
(3) The "mixed" group, of order 2k, generated by A and B, where
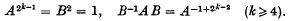
† Math. Ann. 101 (1931), 779.Google Scholar
‡ Proc. London Math. Soc. (2), 40 (1935), 500.Google Scholar
† See Bumside, , Theory of groups, 2nd ed. (Cambridge, 1911), p. 146;Google Scholar types ii, vi.
‡ Hall, , Proc. London Math. Soc. (2), 36 (1932), 39.Google Scholar