Let G be a finite soluble group. In (1) Alperin proves that two system normalizers of G contained in the same Carter subgroup C of G are conjugate in C. In recent unpublished work G.A.Chambers of the University of Wisconsin has proved that, if 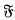is a saturated formation, the 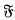-normalizers of an A-group are pronormal subgruops; hence, in particular, that two 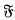-normalizers contained in an 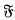-projector E of an A-group are conjugate in E. In this note we describe an example which shows that in Alperin's theorem the class 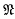of nilpotent groups cannot in general be replaced by an arbitary saturated formation without some restriction on the class of soluble groups under consideration. we prove

PROPOSITION. There exists a saturated formation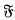and a group G which has two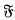-normalizers E1and E2contained in an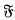-projector F of G such that E1and E2are not conjugate in F.