An asymptotic bound for the residual area of a packing of discs
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose that a sequence of discs
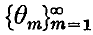
arranged in decreasing order of diameters, forms a packing within the unit plane square I2. It has been shown, by Florian(1), that the area of
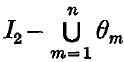
is at least O(a), where a is the radius of θn. However, Gilbert (2) has produced some empirical results for the Apollonius packing 71 of discs which seem to suggest that for such a packing, the area of the set
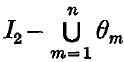
is at least O(as) for some positive real number s, less than one. As Gilbert remarks, it is difficult to imagine that the Apollonius packing is not the extremal case, and so, that it would seem likely that there exists a positive real number s, less than one, such that for a general packing, the area of
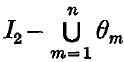
is at least O(as). The purpose of this paper is to establish this result by showing that 0·97 is an allowable value for s.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 4 , October 1966 , pp. 699 - 704
- Copyright
- Copyright © Cambridge Philosophical Society 1966
References
REFERENCES
- 2
- Cited by


