Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bachoc, Christine
Couvreur, Alain
and
Zémor, Gilles
2018.
Towards a function field version of Freiman’s Theorem.
Algebraic Combinatorics,
Vol. 1,
Issue. 4,
p.
501.
Bachoc, Christine
Serra, Oriol
and
Zémor, Gilles
2018.
Revisiting Kneser’s Theorem for Field Extensions.
Combinatorica,
Vol. 38,
Issue. 4,
p.
759.
Niu, Yongfeng
Yue, Qin
and
Wu, Yansheng
2020.
Several kinds of large cyclic subspace codes via Sidon spaces.
Discrete Mathematics,
Vol. 343,
Issue. 5,
p.
111788.
Feng, Tao
and
Wang, Ye
2021.
New constructions of large cyclic subspace codes and Sidon spaces.
Discrete Mathematics,
Vol. 344,
Issue. 4,
p.
112273.
Zhang, He
and
Cao, Xiwang
2022.
Constructions of Sidon spaces and cyclic subspace codes.
Frontiers of Mathematics in China,
Vol. 17,
Issue. 2,
p.
275.
Briaud, Pierre
Tillich, Jean-Pierre
and
Verbel, Javier
2022.
Selected Areas in Cryptography.
Vol. 13203,
Issue. ,
p.
419.
Con, Roni
Shpilka, Amir
and
Tamo, Itzhak
2022.
Reed Solomon Codes Against Adversarial Insertions and Deletions.
p.
2940.
Zhang, Tao
and
Ge, Gennian
2022.
New constructions of Sidon spaces.
Journal of Algebraic Combinatorics,
Vol. 55,
Issue. 3,
p.
781.
LIU, Xue-Mei
SHI, Tong
NIU, Min-Yao
SHEN, Lin-Zhi
and
GAO, You
2023.
New Constructions of Sidon Spaces and Cyclic Subspace Codes.
IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences,
Vol. E106.A,
Issue. 8,
p.
1062.
Zhang, He
and
Tang, Chunming
2023.
Constructions of large cyclic constant dimension codes via Sidon spaces.
Designs, Codes and Cryptography,
Vol. 91,
Issue. 1,
p.
29.
Con, Roni
Shpilka, Amir
and
Tamo, Itzhak
2023.
Reed Solomon Codes Against Adversarial Insertions and Deletions.
IEEE Transactions on Information Theory,
Vol. 69,
Issue. 5,
p.
2991.
Zhang, He
and
Tang, Chunming
2023.
Further constructions of large cyclic subspace codes via Sidon spaces.
Linear Algebra and its Applications,
Vol. 661,
Issue. ,
p.
106.
Castello, Chiara
Polverino, Olga
Santonastaso, Paolo
and
Zullo, Ferdinando
2023.
Constructions and equivalence of Sidon spaces.
Journal of Algebraic Combinatorics,
Vol. 58,
Issue. 4,
p.
1299.
Napolitano, Vito
Polverino, Olga
Santonastaso, Paolo
and
Zullo, Ferdinando
2023.
Classifications and constructions of minimum size linear sets on the projective line.
Finite Fields and Their Applications,
Vol. 92,
Issue. ,
p.
102280.
Zullo, Ferdinando
2023.
Multi-orbit cyclic subspace codes and linear sets.
Finite Fields and Their Applications,
Vol. 87,
Issue. ,
p.
102153.
Zhang, He
Tang, Chunming
and
Hu, Xing
2023.
New constructions of Sidon spaces and large cyclic constant dimension codes.
Computational and Applied Mathematics,
Vol. 42,
Issue. 5,
Li, Yun
and
Liu, Hongwei
2023.
Cyclic constant dimension subspace codes via the sum of Sidon spaces.
Designs, Codes and Cryptography,
Vol. 91,
Issue. 4,
p.
1193.
Zhang, He
Tang, Chunming
and
Cao, Xiwang
2024.
Large optimal cyclic subspace codes.
Discrete Mathematics,
Vol. 347,
Issue. 7,
p.
114007.
Napolitano, Vito
Polverino, Olga
Santonastaso, Paolo
and
Zullo, Ferdinando
2024.
Clubs and Their Applications.
SIAM Journal on Applied Algebra and Geometry,
Vol. 8,
Issue. 3,
p.
493.
Han, Yuqing
and
Cao, Xiwang
2024.
A new construction of cyclic subspace codes.
Cryptography and Communications,
Vol. 16,
Issue. 6,
p.
1527.
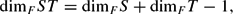 \begin{linenomath}$$
\dim_FST =\dim_F S+\dim_F T-1,
$$\end{linenomath}
\begin{linenomath}$$
\dim_FST =\dim_F S+\dim_F T-1,
$$\end{linenomath}

