Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T14:32:52.372Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebras which represent their linear functionals

Published online by Cambridge University Press:  24 October 2008

F. F. Bonsall  and
A. W. Goldie
F. F. Bonsall
Affiliation:
King's CollegeDurham UniversityNewcastle upon Tyne
A. W. Goldie
Affiliation:
King's CollegeDurham UniversityNewcastle upon Tyne
Get access Rights & Permissions [Opens in a new window]

Extract

This paper was originally intended to contain a generalization of a theorem of Banach on the extension of linear functionals. This generalized theorem now appears as a by-product of a study of a class of algebras which we believe to be of much greater interest than the theorem itself. Let X be a vector space over the real field 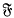and let π(x) be a sub-additive, positive-homogeneous functional on X. Banach ((2), pp. 27–9) proves that any real linear functional f on a subspace X0 of X which satisfies f(x) ≤ π(x) on X0 can be extended to a real linear functional F on X with F(x) ≤ π(x) on X. One of the essential differences between this theorem and the Hahn-Banach theorem is that π can take negative values.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 49 , Issue 1 , January 1953 , pp. 1 - 14
Copyright
Copyright © Cambridge Philosophical Society 1953

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ambrose, W.Structure theorems for a special class of Banach algebras. Trans. Amer. math. Soc. 57 (1945), 364–86.CrossRefGoogle Scholar
(2)Banach, S.Théorie des opérations linéaires (Warsaw, 1932).Google Scholar
(3)Kaplansky, I.Dual rings. Ann. Math., Princeton, (2), 49 (1948), 689–701.CrossRefGoogle Scholar
(4)Kaplansky, I.Normed algebras. Duke math. J. 16 (1949), 399–417.CrossRefGoogle Scholar
(5)Mackey, G. W.On infinite-dimensional linear spaces. Trans. Amer. math. Soc. 57 (1945), 155–207.CrossRefGoogle Scholar
(6)Nachbin, L.A theorem of the Hahn-Banach type for linear transformations. Trans. Amer. math. Soc. 68 (1950), 28–46.CrossRefGoogle Scholar
(7)Nakayama, T.On Frobeniusean algebras I. Ann. Math., Princeton, (2), 40 (1939), 611–33.CrossRefGoogle Scholar
(8)Stone, M. H.Linear transformations in Hilbert space and their applications to analysis (Colloq. Publ. Amer. math. Soc., no. 15, 1932).Google Scholar