Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T18:18:56.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Absorption Probabilities for Sums of Random Variables Defined on a Finite Markov Chain

Published online by Cambridge University Press:  24 October 2008

H. D. Miller
H. D. Miller
Affiliation:
Statistical LaboratoryUniversity of Cambridge
Get access Rights & Permissions [Opens in a new window]

Summary

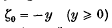This paper is essentially a continuation of the previous one (5) and the notation established therein will be freely repeated. The sequence {ξr} of random variables is defined on a positively regular finite Markov chain {kr} as in (5) and the partial sums and 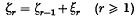are considered. Let ζn be the first positive ζr and let πjk(y), the ‘ruin’ function or absorption probability, be defined by 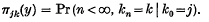The main result (Theorem 1) is an asymptotic expression for πjk(y) for large y in the case when 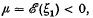, the expectation of ξ1 being computed under the unique stationary distribution for k0, the initial state of the chain, and unconditional on k1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 286 - 298
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bellman, R.On a generalization of the fundamental identity of Wald. Proc. Cambridge Philos. Soc. 53 (1957), 257–259.CrossRefGoogle Scholar
(2)Craméer, H.On some questions connected with mathematical risk. Univ. California Publ. Statist. 2 (1954), 99–124.Google Scholar
(3)Kemperman, J. H. B.The passage problem for a stationary Markov chain (Chicago, 1961).CrossRefGoogle Scholar
(4)Lukacs, E.Characteristic functions (London, 1960).Google Scholar
(5)Miller, H. D.A matrix factorization problem in the theory of random variables defined on a finite Markov chain. Proc. Cambridge Philos. Soc. 58 (1962), 268–285.CrossRefGoogle Scholar
(6)Miller, H. D.A generalization of Wald's identity with applications to random walks. Ann. Math. Statist. 32 (1961), 549–560.CrossRefGoogle Scholar
(7)Miller, H. D.A convexity property in the theory of random variables defined on a finite Markov chain. Ann. Math. Statist. 32 (1961), 1260–1270.CrossRefGoogle Scholar
(8)Noble, B.The Wiener-Hopf technique (London, 1958).Google Scholar
(9)Tweedie, M. C. K.Generalization of Wald's fundamental identity of sequential analysis to Markov chains. Proc. Cambridge Philos. Soc. 56 (1960), 205–214.CrossRefGoogle Scholar
(10)Wald, A.Sequential analysis (New York, 1947).Google Scholar