Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T06:05:12.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Zeroes of the spectral density of the periodic Schrödinger operator with Wigner–von Neumann potential

Published online by Cambridge University Press:  13 December 2011

SERGUEI NABOKO  and
SERGEY SIMONOV
SERGUEI NABOKO
Affiliation:
Department of Mathematical Physics, Institute of Physics, Saint-Petersburg State University, Ulianovskaia 1, St. Petergoff, Saint-Petersburg, 198904Russia. e-mail: [email protected]
SERGEY SIMONOV
Affiliation:
Chebyshev Laboratory, Department of Mathematics and Mechanics, Saint-Petersburg State University, 14th Line, 29b, Saint-Petersburg, 199178Russia. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Schrödinger operator 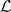α on the half-line with a periodic background potential and the Wigner–von Neumann potential of Coulomb type: csin(2ωx + δ)/(x + 1). It is known that the continuous spectrum of the operator 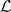α has the same band-gap structure as the free periodic operator, whereas in each band of the absolutely continuous spectrum there exist two points (so-called critical or resonance) where the operator 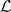α has a subordinate solution, which can be either an eigenvalue or a “half-bound” state. The phenomenon of an embedded eigenvalue is unstable under the change of the boundary condition as well as under the local change of the potential, in other words, it is not generic. We prove that in the general case the spectral density of the operator 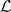α has power-like zeroes at critical points (i.e., the absolutely continuous spectrum has pseudogaps). This phenomenon is stable in the above-mentioned sense.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 1 , July 2012 , pp. 33 - 58
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aronszajn, N.On a problem of Weyl in the theory of singular Sturm–Liouville equations. Amer. J. Math. (3) 79 (1957), 597–610.CrossRefGoogle Scholar
[2]Behncke, H.Absolute continuity of Hamiltonians with von Neumann Wigner potentials I. Proc. Amer. Math. Soc. 111 (1991), 373–384.Google Scholar
[3]Behncke, H.Absolute continuity of Hamiltonians with von Neumann Wigner potentials II. Manuscripta Math. (1) 71 (1991), 163–181.Google Scholar
[4]Behncke, H.The m-function for Hamiltonians with Wigner–von Neumann potentials. J. Math. Phys. (4) 35 (1994), 1445–1462.CrossRefGoogle Scholar
[5]Benzaid, Z. and Lutz, D. A.Asymptotic representation of solutions of perturbed systems of linear difference equations. Stud. Appl. Math. (3) 77 (1987), 195–221.CrossRefGoogle Scholar
[6]Brown, B. M., Eastham, M. S. P. and McCormack, D. K. R.Absolute continuity and spectral concentration for slowly decaying potentials. J. Comput. Appl. Math. 94 (1998), 181–197. arXiv:math/9805025v1.CrossRefGoogle Scholar
[7]Buslaev, V. S. and Matveev, V. B.Wave operators for the Schrödinger equation with a slowly decreasing potential. Theoret. Math. Phys. (3) 2 (1970), 266–274.CrossRefGoogle Scholar
[8]Buslaev, V. S. and Skriganov, M. M.Coordinate asymptotic behavior of the solution of the scattering problem for the Schrödinger equation. Theoret. Math. Phys. (2) 19 (1974), 465–476.Google Scholar
[9]Capasso, F., Sirtori, C., Faist, J., Sivco, D. L., Chu, S. N. G. and Cho, A. Y.Observation of an electronic bound state above a potential well. Nature 358 (1992), 565–567.CrossRefGoogle Scholar
[10]Cruz–Sampedro, J., Herbst, I. and Martinez-Avendano, R.Perturbations of the Wigner-von Neumann potential leaving the embedded eigenvalue fixed. Ann. Henri Poincaré, (2) 3 (2002), 331–345.CrossRefGoogle Scholar
[11]Damanik, D. and Simon, B.Jost functions and Jost solutions for Jacobi matrices, I. A necessary and sufficient condition for Szegő asymptotics. Invent. Math. (1) 165 (2006), 1–50. arXiv:math/0502486v1.CrossRefGoogle Scholar
[12]Deift, P. and Killip, R.On the Absolutely Continuous Spectrum of One-Dimensional Schrödinger Operators with Square Summable Potentials. Comm. Math. Phys. (2) 203 (1999), 341–347.Google Scholar
[13]Gilbert, D. J. and Pearson, D. B.On subordinacy and analysis of the spectrum of one-dimensional Schrödinger operators. J. Math. Anal. Appl. (1) 128 (1987), 30–56.CrossRefGoogle Scholar
[14]Harris, W. A. and Lutz, D. AAsymptotic integration of adiabatic oscillators. J. Math. Anal. Appl. 51 (1975), 76–93.Google Scholar
[15]Hinton, D. B., Klaus, M. and Shaw, J. K.Embedded half-bound states for potentials of Wigner-von Neumann type. Proc. Lond. Math. Soc. (3) 3 (1991), 607–646.CrossRefGoogle Scholar
[16]Janas, J. and Simonov, S.Weyl–Titchmarsh type formula for discrete Schrödinger operator with Wigner–von Neumann potential. Studia Math. (2) 201 (2010), 167–189. arXiv:1003.3319, mp_arc 10-47.CrossRefGoogle Scholar
[17]Kiselev, A.Absolutely continuous spectrum of one-dimensional Schrödinger operators and Jacobi matrices with slowly decreasing potentials. Comm. Math. Phys. (2) 179 (1996), 377–399.Google Scholar
[18]Klaus, M.Asymptotic behavior of Jost functions near resonance points for Wigner-von Neumann type potentials. J. Math. Phys. 32 (1991), 163–174.CrossRefGoogle Scholar
[19]Kodaira, K.The eigenvalue problem for ordinary differential equations of the second order and Heisenberg's theory of S-matrices. Amer. J. Math. (4) 71 (1949), 921–945.CrossRefGoogle Scholar
[20]Kurasov, P.Zero-range potentials with internal structures and the inverse scattering problem. Lett. Math. Phys. (4) 25 (1992), 287–297.CrossRefGoogle Scholar
[21]Kurasov, P.Scattering matrices with finite phase shift and the inverse scattering problem. Inverse Problems (3) 12 (1996), 295–307.Google Scholar
[22]Kurasov, P. and Naboko, S.Wigner–von Neumann perturbations of a periodic potential: spectral singularities in bands. Math. Proc. Camb. Phil. Soc. (1) 142 (2007), 161–183.Google Scholar
[23]Kurasov, P. and Simonov, S.Weyl–Titchmarsh type formula for periodic Schrödinger operator with Wigner–von Neumann potential. Preprints in Mathematical Sciences, Lund University 6 (2010), 1–26.Google Scholar
[24]Matveev, V. B.Wave operators and positive eigenvalues for a Schrödinger equation with oscillating potential. Theoret. Math. Phys. (3) 15 (1973), 574–583.Google Scholar
[25]Naboko, S. N.Dense point spectra of Schrödinger and Dirac operators. Theoret. Math. Phys. (1) 68 (1986), 646–653.CrossRefGoogle Scholar
[26]Nesterov, P. N.Averaging method in the asymptotic integration problem for systems with oscillatory-decreasing coefficients. Differ. Equ. (6) 43 (2007), 745–756.Google Scholar
[27]Simon, B.Some Schrödinger operators with dense point spectrum. Proc. Amer. Math. Soc. (1) 125 (1997), 203–208.Google Scholar
[28]Stone, M. H.Linear Transformations in Hilbert Space (American Mathematical Society, 1932).Google Scholar
[29]Titchmarsh, E. C.Eigenfunction Expansions Associated with Second-Order Differential Equations. Part I (Clarendon Press, 1946).Google Scholar
[30]Titchmarsh, E. C.Eigenfunction Expansions Associated with Second-Order Differential Equations. Part II (Clarendon Press, 1946).Google Scholar
[31]von Neumann, J. and Wigner, E. P.Über merkwürdige diskrete Eigenwerte. Z. Phys. 30 (1929), 465–467.Google Scholar