Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-10T11:44:42.783Z Has data issue: false hasContentIssue false
  • English
  • Français

Wild Galois representations: a family of hyperelliptic curves with large inertia image

Part of: Number theory Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 January 2022

NIRVANA COPPOLA
NIRVANA COPPOLA*
Affiliation:
Vrije Universiteit Amsterdam, De Boelelaan 1111, 1081 HV Amsterdam, The Netherlands. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we generalise the main result of [1] to the family of hyperelliptic curves with potentially good reduction over a p-adic field which have genus 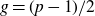$g=({p-1})/{2}$ and the largest possible image of inertia under the 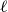$\ell$ -adic Galois representation associated to its Jacobian. We will prove that this Galois representation factors as the tensor product of an unramified character and an irreducible representation of a finite group, which can be either equal to the inertia image (in which case the representation is easily determined) or a 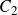$C_2$ -extension of it. In this second case, there are two suitable representations and we will describe the Galois action explicitly in order to determine the correct one.

Keywords

11G2011G20

MSC classification

Primary: 11G20: Curves over finite and local fields
Secondary: 11F80: Galois representations 11F85: $p$-adic theory, local fields 11-04: Explicit machine computation and programs (not the theory of computation or programming)
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 619 - 633
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by EPSRC.

References

Coppola, N.. Wild Galois representations: elliptic curves over a 3-adic field. Acta Arith. 195(3) (2020), 289–303.CrossRefGoogle Scholar
Coppola, N.. Wild Galois representations. https://github.com/NirvanaC93/Wild-Galois-Representations-Magma (2021).Google Scholar
Cornelissen, G.. Two-torsion in the Jacobian of hyperelliptic curves over finite fields. Arch. Math. 77 (2001), 241–246.Google Scholar
Milne, J.S.. Abelian Varieties. G. Cornell, J.H. Silverman, Arithmetic Geometry (Springer-Verlag, 1986).CrossRefGoogle Scholar
Deligne, P.. La conjecture de Weil: I. Publ. Math. Inst. Hautes. études Sci. 43 (1974), 273–307.CrossRefGoogle Scholar
Dokchitser, T. and Dokchitser, V.. Euler factors determine local Weil representations. Crelle 717 (2016), 35–46.Google Scholar
Dokchitser, T., Dokchitser, V., Maistret, C. and Morgan, A.. Arithmetic of hyperelliptic curves over local fields. To appear in Math. Ann.Google Scholar
Dokchitser, T., Dokchitser, V. and Morgan, A.. Tate module and bad reduction. Proc. Amer. Math. Soc. 149 (2021), 1361–1372.CrossRefGoogle Scholar
Dokchitser, T. and Dokchitser, V.. Quotients of hyperelliptic curves and étale cohomology. Quaterly J. Math. 69(2) (2018), 747–768.Google Scholar
Dokchitser, T.. Group names (groupnames.org).Google Scholar
Greenberg, M.J. and Serre, J.P.. Local Fields (Springer, New York, 1995).Google Scholar
Milne, J., Abelian varieties. Arithmetic Geometry vol. 5, (Springer, New York, 1986), 103–150.Google Scholar
Milne, J., Jacobian varieties. Arithmetic Geometry vol. 7, (Springer, New York, 1986), 167–212.Google Scholar
Serre, J.P. and Tate, J.. Good reduction of abelian varieties. Ann. of Math. 88(3) (1968), 492–517.CrossRefGoogle Scholar
Serre, J.P.. Linear Representations of Finite Groups (Springer-Verlag, New York, 1977).CrossRefGoogle Scholar
Yelton, J.. An abelian subextension of the dyadic division field of a hyperelliptic Jacobian. Math. Slovaca 69(2) (2019), 357–370.CrossRefGoogle Scholar