Article contents
When rings of differential operators are maximal orders
Published online by Cambridge University Press: 24 October 2008
Abstract
Let A be a commutative domain, finitely generated as an algebra over a field k of characteristic zero and write 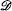 (A) for the ring of k -linear differential operators. Then
(A) for the ring of k -linear differential operators. Then 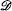 A is an Ore domain with quotient division ring, say Q. Our main result is that
A is an Ore domain with quotient division ring, say Q. Our main result is that 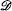 A is a maximal order in Q if and only if (i) A = ∩{Ap: height (p) = 1} and (ii) A is geometrically unibranched. In this case
A is a maximal order in Q if and only if (i) A = ∩{Ap: height (p) = 1} and (ii) A is geometrically unibranched. In this case 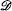 A is also a Krull domain with no reflexive ideals. We also determine some conditions under which
A is also a Krull domain with no reflexive ideals. We also determine some conditions under which 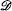 A is simple.
A is simple.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 399 - 410
- Copyright
- Copyright © Cambridge Philosophical Society 1987
References
REFERENCES
- 5
- Cited by


