No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let F be a totally real quartic field. For any α in F, let α, α′, α″, α‴ or α(0) = α(1), α(2), α(3) denote the conjugates of α. Define the function T(α) by
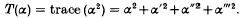
We define a triple of units ε1, ε2, ε3 in F as follows. Let ε1 be a unit which gives the least value of T(ε) for any unit ε ≠ = ± 1 in F. Let ε2 be a unit which gives the least value of T(ε) for any unit ε ≠ = ± ε1m with m a rational integer. Let ε3 be a unit which gives the least value of T(ε) for ε ≠ = ± ε1m ε2n with m and n rational integers. We call ε1, ε2, ε3 the successive unit minima for T(ε).