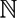Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T08:56:27.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of the maximal ideal of operators on the ℓp-sum of ℓ∞n (n ∈ $\mathbb{N}$) for 1 < p < ∞

Published online by Cambridge University Press:  18 January 2016

TOMASZ KANIA  and
NIELS JAKOB LAUSTSEN
TOMASZ KANIA
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-956 Warszawa, Poland. e-mail: [email protected]
NIELS JAKOB LAUSTSEN
Affiliation:
Department of Mathematics and Statistics, Fylde College, Lancaster University, Lancaster LA1 4YF. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A recent result of Leung (Proceedings of the American Mathematical Society, 2015) states that the Banach algebra ℬ(X) of bounded, linear operators on the Banach space X = (⊕n∈$\mathbb{N}$ ℓ∞n)ℓ1 contains a unique maximal ideal. We show that the same conclusion holds true for the Banach spaces X = (⊕n∈$\mathbb{N}$ ℓ∞n)ℓp and X = (⊕n∈$\mathbb{N}$ ℓ1n)ℓp whenever p ∈ (1, ∞).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 3 , May 2016 , pp. 413 - 421
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Albiac, F. and Kalton, N. J.Topics in Banach Space Theory. Grad. Texts in Math. 233 (Springer–Verlag, New York, 2006).Google Scholar
[2]Androulakis, G. and Schlumprecht, Th.The Banach space S is complementably minimal and subsequentially prime. Studia Math. 156 (2003), 227–242.CrossRefGoogle Scholar
[3]Casazza, P. G., Johnson, W. B. and Tzafriri, L.On Tsirelson's space. Israel J. Math. 47 (1984), 81–98.CrossRefGoogle Scholar
[4]Casazza, P. G. and Odell, E.Tsirelson's space and minimal subspaces. Texas Functional Analysis Seminar 1982–1983. Longhorn Notes (University of Texas Press, Austin, TX 1983), 61–72.Google Scholar
[5]Diestel, J., Jarchow, H. and Tonge, A.Absolutely Summing Operators. Camb. Stud. Adv. Math. 43 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
[6]Dosev, D. and Johnson, W. B.Commutators on ℓ∞. Bull. London Math. Soc. 42 (2010), 155–169.CrossRefGoogle Scholar
[7]Figiel, T. and Johnson, W. B.A uniformly convex Banach space which contains no ℓp. Compositio Math. 29 (1974), 179–190.Google Scholar
[8]Kania, T. and Laustsen, N. J.Uniqueness of the maximal ideal of the Banach algebra of bounded operators on C([0,ω1]). J. Funct. Anal. 262 (2012), 4831–4850.CrossRefGoogle Scholar
[9]Kato, T.Perturbation theory for nullity, deficiency and other quantities of linear operators. J. Anal. Math. 6 (1958), 261–322.CrossRefGoogle Scholar
[10]Laustsen, N. J., Loy, R. J. and Read, C. J.The lattice of closed ideals in the Banach algebra of operators on certain Banach spaces. J. Funct. Anal. 214 (2004), 106–131.CrossRefGoogle Scholar
[11]Laustsen, N. J., Odell, E.Th. Schlumprecht and A. Zsák. Dichotomy theorems for random matrices and closed ideals of operators on (⊕n = 1∞ ℓ1n)c 0. J. London Math. Soc. 86 (2012), 235–258.CrossRefGoogle Scholar
[12]Leung, D.Ideals of operators on (⊕nℓ∞(n))ℓ1. Proc. Amer. Math. Soc. 143 (2015), 3047–3053.CrossRefGoogle Scholar
[13]Lindenstrauss, J. and Tzafriri, L.Classical Banach Spaces I. Ergeb. Math. Grenz-geb. 92 (Springer–Verlag, Berlin–New York, 1977).CrossRefGoogle Scholar
[14]Pełczyński, A.Projections in certain Banach spaces. Studia Math. 19 (1960), 209–228.CrossRefGoogle Scholar
[15]Stephani, I.Operator ideals generalizing the ideal of strictly singular operators. Math. Nachr. 94 (1980), 29–41.CrossRefGoogle Scholar