Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T20:01:26.588Z Has data issue: false hasContentIssue false
  • English
  • Français

The Uniqueness of a Certain Trigonometric Integral

Published online by Cambridge University Press:  24 October 2008

A. C. Offord
A. C. Offord
Affiliation:
St John's College[Communicated by Prof. G. H. Hardy]
Get access Rights & Permissions [Opens in a new window]

Extract

Verblunsky has recently proved the following theorem:

Theorem A. Suppose that

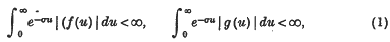
for every positive σ. Write

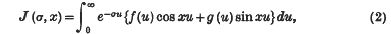
and suppose that J (σ, x) is bounded in σ, x for σ > 0 and all x. Then

exists almost everywhere, and

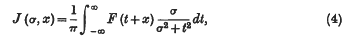
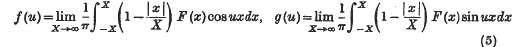
almost everywhere.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 31 , Issue 3 , July 1935 , pp. 382 - 389
Copyright
Copyright © Cambridge Philosophical Society 1935

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 382 note * Verblunsky, S., “Trigonometric integrals and harmonic functions”, Proc. London Math. Soc. (2), 38 (1934), 1–48 (19)Google Scholar. Verblunsky does not state the hypothesis (1) explicitly in the enunciation of his theorem, but it is understood throughout the paper. It is employed in the proof of this particular theorem on p. 20.

page 382 note † Offord, A. C., “On Fourier transforms”, Proc. London Math. Soc. (2), 38 (1934), 197–216Google Scholar, and “On Fourier transforms (II)”, ibid., in the press. We refer to these papers as I and II respectively.

page 385 note * See, for example, Hardy, and Riesz, , The general theory of Dirichlet's series, p. 29Google Scholar. The proofs for series and integrals are the same.