Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T23:50:09.185Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniformly bounded components of normality

Published online by Cambridge University Press:  01 July 2007

XIAOLING WANG  and
WANG ZHOU
XIAOLING WANG
Affiliation:
Department of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing 210046, Jiangsu, China. e-mail: [email protected]
WANG ZHOU
Affiliation:
Department of Statistics and Applied Probability, National University of Singapore, Singapore, 117546. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that f(z) is a transcendental entire function and that the Fatou set F(f)≠∅. Set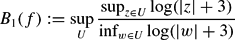and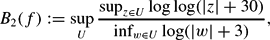where the supremum supU is taken over all components of F(f). If B1(f)<∞ or B2(f)<∞, then we say F(f) is strongly uniformly bounded or uniformly bounded respectively. We show that, under some conditions, F(f) is (strongly) uniformly bounded.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 143 , Issue 1 , July 2007 , pp. 85 - 101
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anderson, J. M. and Hinkkanen, A.. Unbounded domains of normality. Proc. Amer. Math. Soc. 126 (1998), no. 4, 3243–3252.CrossRefGoogle Scholar
[2]Baker, I. N.. Multiply connected domains of normality in iteration theory. Math. Z. 81 (1963), 206–214.CrossRefGoogle Scholar
[3]Baker, I. N.. Multiply connected domains of normality in iteration theory. Ann. Acad. Sci. Fenn. Ser. A.I. Math. 1 (1975), 277–283.CrossRefGoogle Scholar
[4]Baker, I. N.. The iteration of polynomials and transcendental entire functions. J. Austral. Math. Soc. Ser.A 30 (1981), 483–495.CrossRefGoogle Scholar
[5]Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. London Math. Soc. 49 (1984), 563–576.CrossRefGoogle Scholar
[6]Baker, I. N.. Some entire functions with multiply connected wandering domains. Ergod. Th. Dynam. Sys. 5 (1985), 163–169.CrossRefGoogle Scholar
[7]Barry, P. D.. On the theorem of Besicovitch. Quart. J. Math. Oxford 14 (1963), 292–302.CrossRefGoogle Scholar
[8]Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151–188.CrossRefGoogle Scholar
[9]Carleson, L. and Gamelin, T. W.. Complex Dynamics (Springer-Verlag 1993).CrossRefGoogle Scholar
[10]Fatou, P.. Sur l' itération des fonctions transcendentes entières. Acta Math. 47 (1926), 337–370.CrossRefGoogle Scholar
[11]Fuchs, W. H. J.. Proof of a conjecture of Polya concerning gap series. Illinois J. Math. 7 (1966), 661–667.Google Scholar
[12]Hua, X. H. and Yang, C. C.. Dynamics of Transcendental Functions (Gordon and Breach Science Publishers 1998).Google Scholar
[13]Hua, X. H. and Yang, C. C.. Fatou components of entire functions of small growth. Ergod. Th. Dynam. Sys. 19 (1999), 1281–1293.CrossRefGoogle Scholar
[14]Julia, G.. Mémoire sur l' iteration des fractions rationnelles. J. Math. Pures Appl. 1 (1918), 47–245.Google Scholar
[15]Kisaka, M. and Shishikura, M.. On multiply connected wandering domains of entire functions. To appear.Google Scholar
[16]Morosawa, S., Nishimura, Y., Taniguchi, M. and Ueda, T.. Holomorphic Dynamics (Cambridge University Press, 2000).Google Scholar
[17]Rempe, L.. Siegel disks and periodic rays of entire functions. Preprint.Google Scholar
[18]Stallard, G. M.. The iteration of entire functions of small growth. Math. Proc. Camb. Phil. Soc. 114 (1993), 43–55.CrossRefGoogle Scholar
[19]Wang, X. L. and Yang, C. C.. On the wandering and Baker domains of transcendental entire functions. Intern. J. Bifur. Chaos. 14 (2004), no. 1, 321–327.CrossRefGoogle Scholar
[20]Wang, Y. F.. Bounded domains of the Fatou set of an entire function. Israel J. Math. 121 (2001), 55–60.CrossRefGoogle Scholar
[21]Wang, Y. F.. On the Fatou set of an entire function with gaps. Tohoku Math. J. 53 (2001), 163–170.CrossRefGoogle Scholar
[22]Zheng, J. H.. Singularities and wandering domains in iteration of meromorphic functions. Illinois J. Math. 44 (2000), 520–530.CrossRefGoogle Scholar
[23]Zheng, J. H.. On the non-existence of unbounded domains of normality of meromorphic functions. J. Math. Anal. Appl. 264 (2001), 479–494.Google Scholar
[24]Zheng, J. H.. On uniformly perfect boundary of stable domains in iteration of meromorphic functions II. Math. Proc. Camb. Phil. Soc. 132 (2002), 531–544.Google Scholar
[25]Zheng, J. H.. Singularities and limit functions in iteration of meromorphic functions. J. London Math. Soc. 67 (2003), 1–13.CrossRefGoogle Scholar
[26]Zheng, J. H. and Wang, S.. Boundedness of components of Fatou sets of entire and meromorphic functions. Indian J. Pure Appl. Math. 35 (2004), no. 10, 1137–1148.Google Scholar
[27]Zheng, J. H.. On multiply connected Fatou components in iteration of meromorphic functions. J. Math. Anal. Appl. 313 (2006), no. 1, 24–37.CrossRefGoogle Scholar