Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T13:27:19.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional elastic inclusion problems

Published online by Cambridge University Press:  24 October 2008

R. D. List  and
J. P. O. Silberstein
R. D. List
Affiliation:
University of Western Australia
J. P. O. Silberstein
Affiliation:
University of Western Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

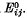A system of equations is derived for determining the elastic fields in an inclusion and its surrounding finite matrix when the inclusion suffers a physical change and, if not constrained by the matrix, would undergo a deformation . A method for obtaining the exact solution of these equations, when the matrix and inclusion have the same elastic constants, is described and the particular problem of the square inclusion in an infinite matrix solved.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 2 , April 1966 , pp. 303 - 311
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bhargava, R. D.The inclusion problem, Applied Scientific Research, Section A, vol. 11 (1962), No. 1, pp. 80–84. The Hague, Martinus Nijhoff (publisher).Google Scholar
(2)Eshelby, J. D.Proc. Roy. Soc. Ser. A, 241 (1957), 376.Google Scholar
(3)Eshelby, J. D.Proc. Roy. Soc. Ser. A, 252 (1959), 561.Google Scholar
(4)Jaswon, M. A. and Bhargava, R. D.Proc. Cambridge Philos. Soc. 57 (1961), 669.CrossRefGoogle Scholar
(5)Muskhelishvili, N. I.Some basic problems of the mathematical theory of elasticity (Noordhoff; Groningen, Holland, 1953).Google Scholar
(6)Sherman, D. I.On the problem of plane strain in non-homogeneous media. Non-homogeneity in elasticity and plasticity (Pergamon Press, 1959).Google Scholar